Question

The joint equation of the pair of lines through the origin and forming an equilateral triangle with 3x + 4y = 5 is:

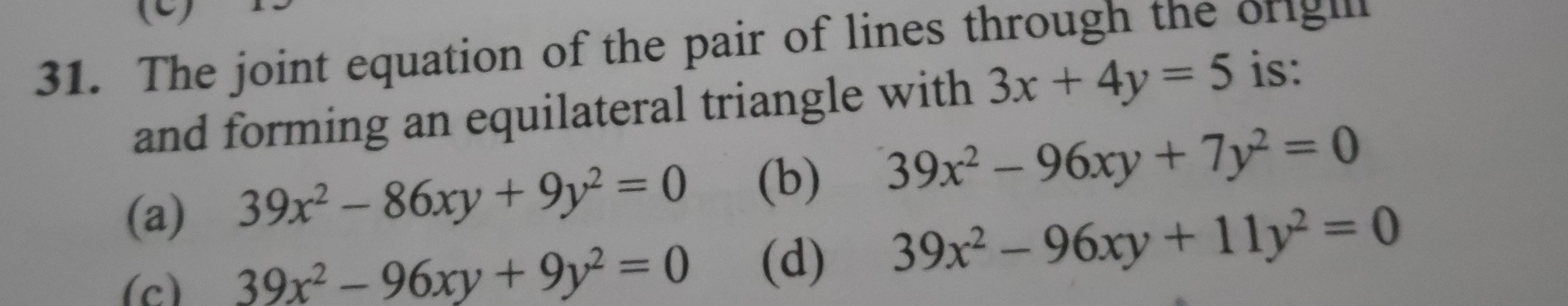
• A. $39x^2 - 86xy + 9y^2 = 0$
• B. $39x^2 - 96xy + 7y^2 = 0$
• C. $39x^2 - 96xy + 9y^2 = 0$
• D. $39x^2 - 96xy + 11y^2 = 0$

Answer 1

Answer: (D)

39x^2 - 96xy + 11y^2 = 0

Answer 2

The problem asks for the joint equation of a pair of lines passing through the origin that form an equilateral triangle with the line $3x + 4y = 5$.

Let the given line be $L_1: 3x + 4y = 5$. The slope of this line is $m_1 = -\frac{3}{4}$. Let the pair of lines through the origin be $L_2$ and $L_3$. Their joint equation will be of the form $Ax^2 + 2Hxy + By^2 = 0$. Since the triangle formed by $L_1, L_2, L_3$ is equilateral, the angle between any two of these lines must be $60^\circ$. This means the angle between $L_2$ and $L_3$ is $60^\circ$. Also, the angle between $L_1$ and $L_2$ is $60^\circ$, and the angle between $L_1$ and $L_3$ is $60^\circ$.

Let $m$ be the slope of one of the lines from the pair ($L_2$ or $L_3$). The angle between this line (with slope $m$) and $L_1$ (with slope $m_1 = -3/4$) is $60^\circ$. The formula for the angle $\theta$ between two lines with slopes $m_a$ and $m_b$ is $\tan \theta = \left| \frac{m_a - m_b}{1 + m_a m_b} \right|$. Substituting the values: $\tan 60^\circ = \left| \frac{m - (-\frac{3}{4})}{1 + m(-\frac{3}{4})} \right|$ $\sqrt{3} = \left| \frac{m + \frac{3}{4}}{1 - \frac{3}{4}m} \right|$

To remove the absolute value and the square root, we square both sides: $(\sqrt{3})^2 = \left( \frac{4m + 3}{4 - 3m} \right)^2$ $3 = \frac{(4m + 3)^2}{(4 - 3m)^2}$ $3(4 - 3m)^2 = (4m + 3)^2$ Expand both sides: $3(16 - 24m + 9m^2) = 16m^2 + 24m + 9$ $48 - 72m + 27m^2 = 16m^2 + 24m + 9$

Rearrange the terms to form a quadratic equation in $m$: $27m^2 - 16m^2 - 72m - 24m + 48 - 9 = 0$ $11m^2 - 96m + 39 = 0$

This quadratic equation gives the slopes of the two lines $L_2$ and $L_3$. Let these slopes be $m_2$ and $m_3$. For a quadratic equation $am^2 + bm + c = 0$, the sum of roots is $m_2 + m_3 = -b/a$ and the product of roots is $m_2 m_3 = c/a$. From $11m^2 - 96m + 39 = 0$: $m_2 + m_3 = \frac{-(-96)}{11} = \frac{96}{11}$ $m_2 m_3 = \frac{39}{11}$

The lines $L_2$ and $L_3$ pass through the origin, so their equations are $y = m_2 x$ and $y = m_3 x$. The joint equation of these two lines is $(y - m_2 x)(y - m_3 x) = 0$. Expanding this, we get: $y^2 - (m_2 + m_3)xy + m_2 m_3 x^2 = 0$

Substitute the values of $m_2 + m_3$ and $m_2 m_3$: $y^2 - \left(\frac{96}{11}\right)xy + \left(\frac{39}{11}\right)x^2 = 0$

To clear the denominators, multiply the entire equation by 11: $11y^2 - 96xy + 39x^2 = 0$

Rearranging in the standard form $Ax^2 + 2Hxy + By^2 = 0$: $39x^2 - 96xy + 11y^2 = 0$

This matches option (d).