Question
Question: Let $|\bar{A}_1| = 3, |\bar{A}_2| = 5$ and $|\bar{A}_1 + \bar{A}_2| = 5$. The value of $(2\bar{A}_1 ...
Let ∣Aˉ1∣=3,∣Aˉ2∣=5 and ∣Aˉ1+Aˉ2∣=5. The value of (2Aˉ1+3Aˉ2).(3Aˉ1−2Aˉ2) is :-
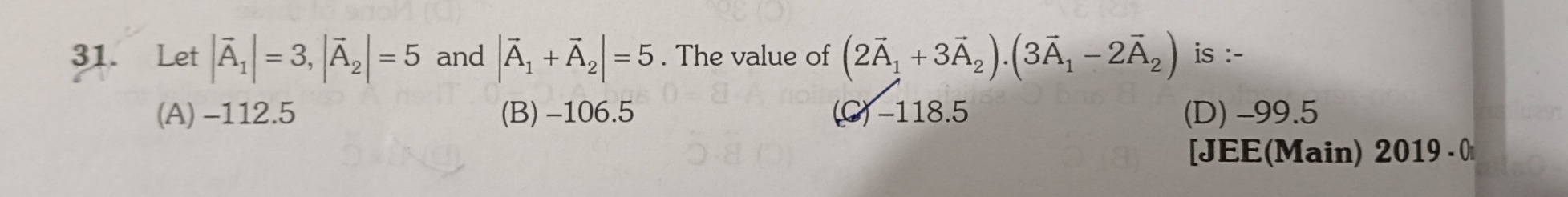
-112.5
-106.5
-118.5
-99.5
-118.5
Solution
To solve the problem, we first need to find the dot product of Aˉ1 and Aˉ2 using the given magnitudes.
Given: ∣Aˉ1∣=3 ∣Aˉ2∣=5 ∣Aˉ1+Aˉ2∣=5
We know the formula for the magnitude of the sum of two vectors: ∣Aˉ1+Aˉ2∣2=∣Aˉ1∣2+∣Aˉ2∣2+2Aˉ1⋅Aˉ2
Substitute the given values into the formula: 52=32+52+2Aˉ1⋅Aˉ2 25=9+25+2Aˉ1⋅Aˉ2 25=34+2Aˉ1⋅Aˉ2
Now, solve for 2Aˉ1⋅Aˉ2: 2Aˉ1⋅Aˉ2=25−34 2Aˉ1⋅Aˉ2=−9 Aˉ1⋅Aˉ2=−29=−4.5
Next, we need to evaluate the expression (2Aˉ1+3Aˉ2).(3Aˉ1−2Aˉ2). We can expand this dot product using the distributive property, similar to algebraic multiplication: (2Aˉ1+3Aˉ2).(3Aˉ1−2Aˉ2)=(2Aˉ1)⋅(3Aˉ1)+(2Aˉ1)⋅(−2Aˉ2)+(3Aˉ2)⋅(3Aˉ1)+(3Aˉ2)⋅(−2Aˉ2) =6(Aˉ1⋅Aˉ1)−4(Aˉ1⋅Aˉ2)+9(Aˉ2⋅Aˉ1)−6(Aˉ2⋅Aˉ2)
Recall that Aˉ⋅Aˉ=∣Aˉ∣2 and Aˉ1⋅Aˉ2=Aˉ2⋅Aˉ1. So, the expression becomes: =6∣Aˉ1∣2−4(Aˉ1⋅Aˉ2)+9(Aˉ1⋅Aˉ2)−6∣Aˉ2∣2 Combine the terms with Aˉ1⋅Aˉ2: =6∣Aˉ1∣2+5(Aˉ1⋅Aˉ2)−6∣Aˉ2∣2
Now, substitute the known values: ∣Aˉ1∣=3, ∣Aˉ2∣=5, and Aˉ1⋅Aˉ2=−4.5: =6(32)+5(−4.5)−6(52) =6(9)+(−22.5)−6(25) =54−22.5−150 =54−172.5 =−118.5
