Question

$\int 2 \frac{cos^2 x - sin^2 x}{cos^2 x + sin^2 x} dx =$

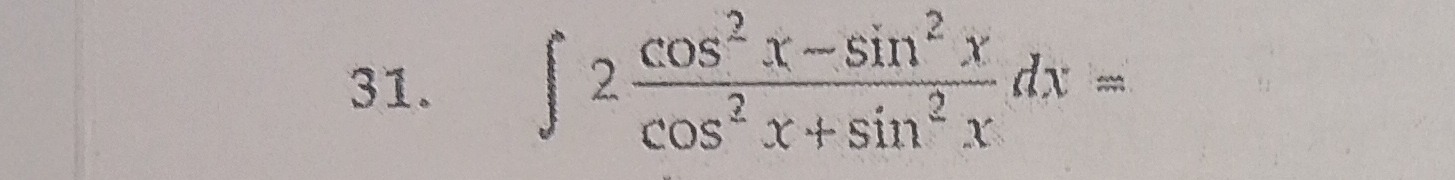
Answer 1

$\sin2x+C$

Answer 2

We start with the integral

$$\int 2\frac{\cos^2 x - \sin^2 x}{\cos^2 x + \sin^2 x}\,dx.$$

Since $\cos^2 x + \sin^2 x = 1$, the expression simplifies to

$$\int 2(\cos^2x - \sin^2x)\,dx.$$

Recall the double-angle identity: $\cos 2x = \cos^2 x - \sin^2 x$. Thus, the integral is

$$\int 2\cos2x\,dx.$$

Integrating, we have

$$\int 2\cos2x\,dx = 2\cdot\frac{1}{2}\sin2x = \sin2x + C.$$

Minimal Explanation:

Use $\cos^2x+\sin^2x=1$ and $\cos2x=\cos^2x-\sin^2x$ to simplify the integral to $\int 2\cos2x\,dx$, which integrates to $\sin2x+C$.