Question
Question: In a series $LCR$ circuit, voltage across $R$ is 100V and $R = 1k\Omega$ with $C = 2\mu F$. The reso...
In a series LCR circuit, voltage across R is 100V and R=1kΩ with C=2μF. The resonant frequency ω is 200 rad/s. At resonance the voltage across L is
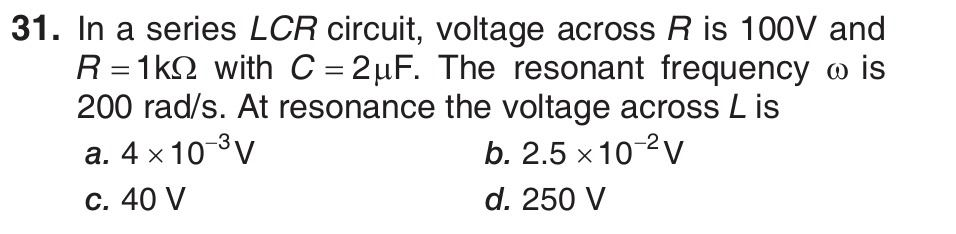
4×10−3V
2.5×10−2V
40 V
250 V
250 V
Solution
In a series LCR circuit at resonance, the inductive reactance (XL) is equal to the capacitive reactance (XC).
XL=XC=ωC1
The current flowing through the circuit at resonance can be found using the voltage across the resistor (VR) and the resistance (R). Since it's a series circuit, the same current flows through all components.
Given VR=100 V and R=1 kΩ=1000 Ω.
The current I is given by Ohm's law:
I=RVR=1000 Ω100 V=0.1 A
The voltage across the inductor (VL) is given by the product of the current (I) and the inductive reactance (XL).
VL=I×XL
At resonance, XL=XC=ωC1.
Given ω=200 rad/s and C=2 μF =2×10−6 F.
Calculate the capacitive reactance XC:
XC=ωC1=(200 rad/s)×(2×10−6 F)1=400×10−61=4×10−41
XC=4104=2500 Ω
Since XL=XC at resonance, XL=2500 Ω.
Now calculate the voltage across the inductor VL:
VL=I×XL=(0.1 A)×(2500 Ω)=250 V
The voltage across the inductor at resonance is 250 V.
