Question

G (3,-5, r) is centroid of triangle ABC where A (7, -8, 1), B (p,q, 5) and C (q + 1, 5p, 0) are vertices of triangle then values of p, q, r are respectively.

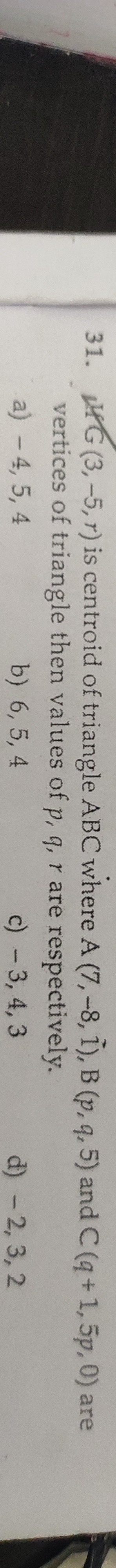
• A.
  • 4, 5, 4
• B. 6, 5, 4
• C.
  • 3, 4, 3
• D.
  • 2, 3, 2

Answer 1

Answer: (D)

• 2, 3, 2

Answer 2

The centroid G of triangle ABC is given by

$$G = \left(\frac{x_A+x_B+x_C}{3}, \frac{y_A+y_B+y_C}{3}, \frac{z_A+z_B+z_C}{3}\right)$$

Given:

$A = (7,-8,1)$

$B = (p,q,5)$

$C = (q+1, 5p, 0)$

$G = (3,-5,r)$

1. x-coordinate:

$$\frac{7+p+(q+1)}{3} = 3 \quad \Rightarrow \quad \frac{p+q+8}{3}=3 \quad \Rightarrow \quad p+q+8=9 \quad \Rightarrow \quad p+q=1 \quad \text{(1)}$$

2. y-coordinate:

$$\frac{-8+q+5p}{3} = -5 \quad \Rightarrow \quad 5p+q-8 = -15 \quad \Rightarrow \quad 5p+q = -7 \quad \text{(2)}$$

3. z-coordinate:

$$\frac{1+5+0}{3} = r \quad \Rightarrow \quad \frac{6}{3} = r \quad \Rightarrow \quad r=2$$

Subtract equation (1) from (2):

$$(5p+q) - (p+q) = -7 - 1 \quad \Rightarrow \quad 4p = -8 \quad \Rightarrow \quad p = -2$$

Substitute $p = -2$ into equation (1):

$$-2 + q = 1 \quad \Rightarrow \quad q = 3$$

Thus, $p = -2$, $q = 3$, $r=2$.