Question

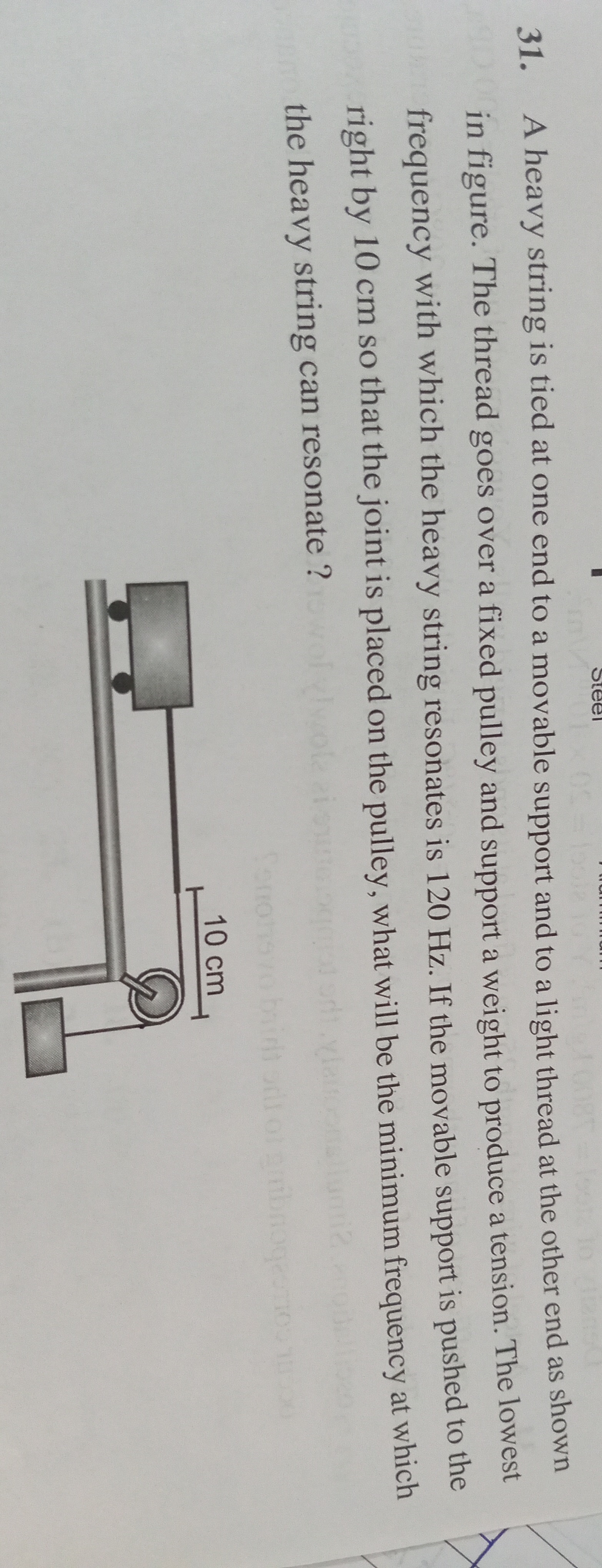
A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in figure. The thread goes over a fixed pulley and support a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate ?

Answer 1

240 Hz

Answer 2

The heavy string is fixed at both ends: at the movable support and at the pulley (where it is connected to the light thread). Let the initial length of the heavy string be $L_1$. The speed of transverse waves in the string is $v = \sqrt{\frac{T}{\mu}}$, where $T$ is the tension and $\mu$ is the linear mass density. The resonance frequencies for a string fixed at both ends are given by $f_n = \frac{nv}{2L_1} = \frac{n}{2L_1}\sqrt{\frac{T}{\mu}}$, where $n = 1, 2, 3, \dots$. The lowest frequency is the fundamental frequency, which corresponds to $n=1$: $f_1 = \frac{1}{2L_1}\sqrt{\frac{T}{\mu}}$. We are given that the lowest frequency is $120$ Hz, so $f_1 = 120$ Hz.

The movable support is pushed to the right by $10$ cm. From the figure, the movable support is to the left of the pulley. Pushing it to the right means moving it towards the pulley. The initial length of the heavy string is the distance from the movable support to the pulley. Let the initial position of the movable support be $x_1$ and the position of the pulley be $x_p$. The initial length is $L_1 = x_p - x_1$. The movable support is pushed to the right by $10$ cm, so its new position is $x_2 = x_1 + 10$ cm. The heavy string is now between the new position of the movable support and the pulley. The new length of the heavy string is $L_2 = x_p - x_2 = x_p - (x_1 + 10) = (x_p - x_1) - 10 = L_1 - 10$ cm. So, the new length of the heavy string is $L_2 = L_1 - 10$.

In the new setup, the heavy string is still fixed at both ends, with length $L_2$. The tension $T$ and linear mass density $\mu$ remain unchanged. The minimum frequency at which the heavy string can resonate is the new fundamental frequency, $f'_1$. $f'_1 = \frac{1}{2L_2}\sqrt{\frac{T}{\mu}} = \frac{1}{2(L_1 - 10)}\sqrt{\frac{T}{\mu}}$.

We have the initial fundamental frequency $f_1 = \frac{1}{2L_1}\sqrt{\frac{T}{\mu}} = 120$ Hz. From this, we can write $\sqrt{\frac{T}{\mu}} = 2 \times 120 \times L_1 = 240 L_1$. Substitute this into the expression for $f'_1$: $f'_1 = \frac{1}{2(L_1 - 10)}(240 L_1) = \frac{120 L_1}{L_1 - 10}$.

Let's assume the initial length of the heavy string is $L_1$ and the final length is $L_2$. The movable support is pushed to the right by $10$ cm, which means the length of the string is reduced by $10$ cm, so $L_2 = L_1 - 10$. We are given $f_1 = 120$ Hz. We want to find $f'_1$. $f_1 \propto \frac{1}{L_1}$ and $f'_1 \propto \frac{1}{L_2}$. $\frac{f'_1}{f_1} = \frac{L_1}{L_2} = \frac{L_1}{L_1 - 10}$. $f'_1 = 120 \times \frac{L_1}{L_1 - 10}$.

Let's assume from the figure that the initial length of the heavy string is $L_1$ and the movable support is moved by $10$ cm to the right, and the new length is $L_2$. The figure shows the movement of $10$ cm. Let's assume the initial length is $L_1$ and the final length is $L_2$. The movement is $10$ cm. If the movement is towards the pulley, $L_2 = L_1 - 10$.

Let's assume the initial length is $L_1$ and the final length is $L_2$. The movement is $10$ cm. If the initial length was $L_1$ and the final length is $L_2$, and $L_1 = 2L_2$, and the movement is $10$ cm, then $L_1 - L_2 = 10$, so $2L_2 - L_2 = 10$, which means $L_2 = 10$ cm and $L_1 = 20$ cm.

If we assume $L_1 = 20$ cm, then $L_2 = 20 - 10 = 10$ cm. $f'_1 = 120 \frac{20}{20 - 10} = 120 \frac{20}{10} = 120 \times 2 = 240$ Hz.

Therefore, the minimum frequency at which the heavy string can resonate is 240 Hz.