Question

A circle touches the line $x+y-2=0$ at (1, 1) and cuts the circle $x^2+y^2+4x+5y-6=0$ at P and Q. Then :

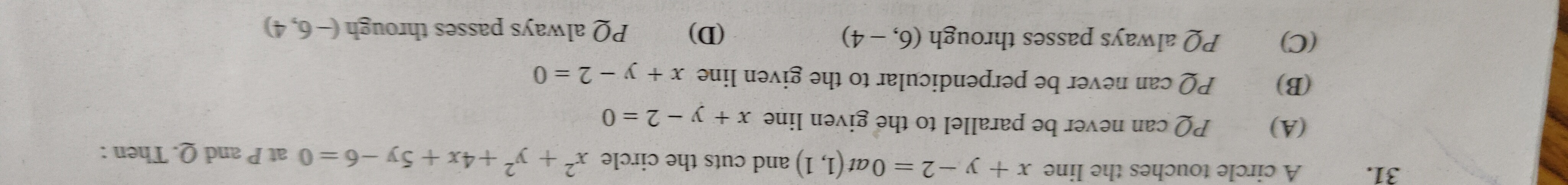
• A. $\overline{PQ}$ can never be parallel to the given line $x+y-2=0$
• B. $\overline{PQ}$ can never be perpendicular to the given line $x+y-2=0$
• C. $\overline{PQ}$ always passes through (6, -4)
• D. $\overline{PQ}$ always passes through (-6, 4)

Answer 1

Answer: (A), (C)

A, C

Answer 2

Let $C_1$ be the circle touching the line $L: x+y-2=0$ at $A(1,1)$, and $C_2$ be the circle $x^2+y^2+4x+5y-6=0$. The common chord of $C_1$ and $C_2$ is $\overline{PQ}$.

1. Equation of $C_1$: The center of $C_1$ lies on the line perpendicular to $L$ at $(1,1)$. The slope of $L$ is $-1$, so the perpendicular line has a slope of $1$. Its equation is $y-1 = 1(x-1)$, which simplifies to $y=x$. Let the center of $C_1$ be $(h,h)$. The radius $r_1 = \sqrt{(h-1)^2 + (h-1)^2} = \sqrt{2}|h-1|$. The equation of $C_1$ is $(x-h)^2 + (y-h)^2 = 2(h-1)^2$, which expands to $x^2+y^2 - 2hx - 2hy + 4h - 2 = 0$.

2. Equation of common chord $\overline{PQ}$: The equation of the common chord is $S_1 - S_2 = 0$. $(x^2+y^2 - 2hx - 2hy + 4h - 2) - (x^2+y^2+4x+5y-6) = 0$ $(-2h-4)x + (-2h-5)y + (4h+4) = 0$ Multiplying by $-1$: $(2h+4)x + (2h+5)y - (4h+4) = 0$.

3. Analysis of options: The equation of $\overline{PQ}$ can be written as $h(2x+2y-4) + (4x+5y-4) = 0$. This is a pencil of lines passing through the intersection of $2x+2y-4=0$ and $4x+5y-4=0$. Solving these equations: From $2x+2y-4=0 \implies x+y-2=0 \implies y=2-x$. Substitute into the second equation: $4x+5(2-x)-4 = 0 \implies 4x+10-5x-4 = 0 \implies -x+6=0 \implies x=6$. Then $y=2-6=-4$. The intersection point is $(6,-4)$.

   • Option (A): The slope of $L$ is $-1$. The slope of $\overline{PQ}$ is $m_{PQ} = -\frac{2h+4}{2h+5}$. For parallel lines, $m_{PQ} = -1$. $-\frac{2h+4}{2h+5} = -1 \implies 2h+4 = 2h+5 \implies 4=5$, which is impossible. Thus, $\overline{PQ}$ is never parallel to $L$. (Correct)

   • Option (B): For perpendicular lines, $m_{PQ} \times (-1) = -1 \implies m_{PQ} = 1$. $-\frac{2h+4}{2h+5} = 1 \implies -(2h+4) = 2h+5 \implies -2h-4 = 2h+5 \implies 4h = -9 \implies h = -9/4$. This is a possible value for $h$, so $\overline{PQ}$ can be perpendicular to $L$. (Incorrect)

   • Option (C): As shown above, the common chord $\overline{PQ}$ always passes through the fixed point $(6,-4)$. (Correct)

   • Option (D): $\overline{PQ}$ passes through $(6,-4)$, not $(-6,4)$. (Incorrect)

Therefore, options (A) and (C) are correct. The common chord $\overline{PQ}$ always passes through the point $(6,-4)$, which is the intersection of the radical axis of the two circles and the line perpendicular to the tangent at the point of contact. The slope of $\overline{PQ}$ is $m_{PQ} = -\frac{2h+4}{2h+5}$. For $\overline{PQ}$ to be parallel to $x+y-2=0$ (slope $-1$), we would need $-\frac{2h+4}{2h+5} = -1$, which leads to $4=5$, an impossibility. Thus, $\overline{PQ}$ can never be parallel to the given line.