Solveeit Logo
Login

Question

Question: $\lim_{x \to 0}\frac{e-(1+2x)^{\frac{1}{2x}}}{x}$ is equal to...

lim⁡x→0e−(1+2x)12xx\lim_{x \to 0}\frac{e-(1+2x)^{\frac{1}{2x}}}{x} is equal to

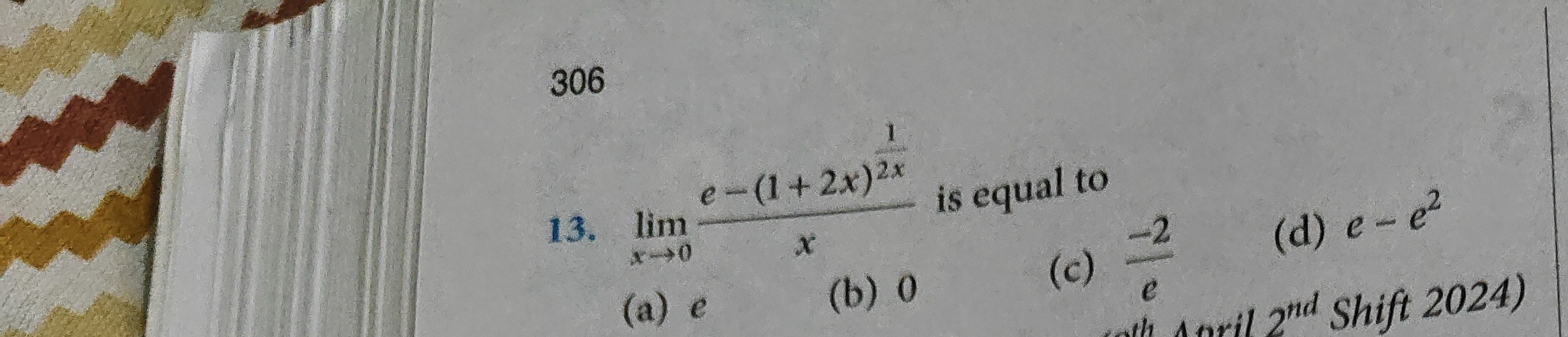
A

e

B

0

C

−2e\frac{-2}{e}

D

e-e²

Answer

e

Explanation

Solution

Let y=(1+2x)12xy = (1+2x)^{\frac{1}{2x}}. We use the Taylor expansion of ln⁡y=12xln⁡(1+2x)\ln y = \frac{1}{2x}\ln(1+2x). Using ln⁡(1+u)=u−u22+O(u3)\ln(1+u) = u - \frac{u^2}{2} + O(u^3), we get ln⁡(1+2x)=2x−(2x)22+O(x3)=2x−2x2+O(x3)\ln(1+2x) = 2x - \frac{(2x)^2}{2} + O(x^3) = 2x - 2x^2 + O(x^3). So, ln⁡y=12x(2x−2x2+O(x3))=1−x+O(x2)\ln y = \frac{1}{2x}(2x - 2x^2 + O(x^3)) = 1 - x + O(x^2). Exponentiating, y=e1−x+O(x2)=e⋅e−x+O(x2)y = e^{1-x+O(x^2)} = e \cdot e^{-x+O(x^2)}. Using ez=1+z+O(z2)e^z = 1+z+O(z^2), we get y=e(1+(−x+O(x2))+O(x2))=e(1−x+O(x2))=e−ex+O(x2)y = e(1 + (-x+O(x^2)) + O(x^2)) = e(1-x+O(x^2)) = e - ex + O(x^2). The limit becomes lim⁡x→0e−(e−ex+O(x2))x=lim⁡x→0ex−O(x2)x=lim⁡x→0(e−O(x))=e\lim_{x \to 0}\frac{e - (e - ex + O(x^2))}{x} = \lim_{x \to 0}\frac{ex - O(x^2)}{x} = \lim_{x \to 0}(e - O(x)) = e.