Question

The locus of points of intersection of the tangents to $x^2 + y^2 = a^2$ at the extremities of a chord of circle $x^2 + y^2 = a^2$ which touches the circle $x^2 + y^2 - 2ax = 0$ is(are);

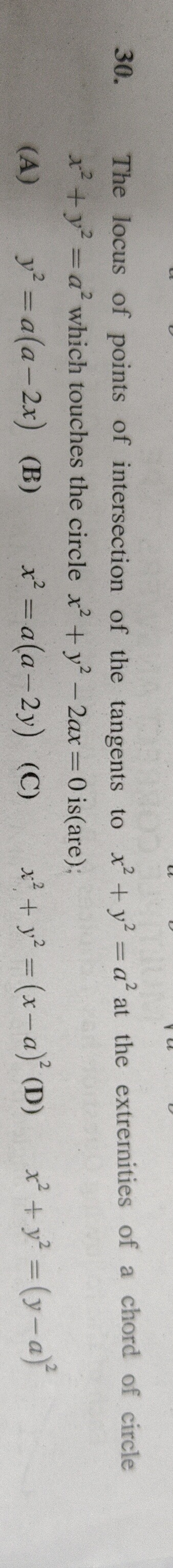
• A. y^2 = a(a-2x)
• B. x^2 = a(a-2y)
• C. x^2 + y^2 = (x-a)^2
• D. x^2 + y^2 = (y-a)^2

Answer 1

Answer: (A), (C)

A, C

Answer 2

Let $P(h, k)$ be the point of intersection of tangents to $x^2 + y^2 = a^2$. The chord of contact from $P(h, k)$ to $x^2 + y^2 = a^2$ is $xh + yk = a^2$. This chord touches the circle $x^2 + y^2 - 2ax = 0$, which is $(x-a)^2 + y^2 = a^2$ with center $(a, 0)$ and radius $a$. The condition for tangency is that the distance from $(a, 0)$ to $xh + yk - a^2 = 0$ equals $a$. This leads to $\frac{|ah - a^2|}{\sqrt{h^2 + k^2}} = a$. Squaring and simplifying gives $k^2 = a^2 - 2ah$. Replacing $(h, k)$ with $(x, y)$ yields the locus $y^2 = a^2 - 2ax$. Options (A) $y^2 = a(a-2x)$ and (C) $x^2 + y^2 = (x-a)^2$ (which simplifies to $y^2 = a^2 - 2ax$) both represent this locus.