Question
Question: 30. $\sqrt[3]{y\sqrt{x}}=\sqrt[6]{(x+y)^2}$, then $\frac{dy}{dx}$ is...
- 3yx=6(x+y)2, then dxdy is
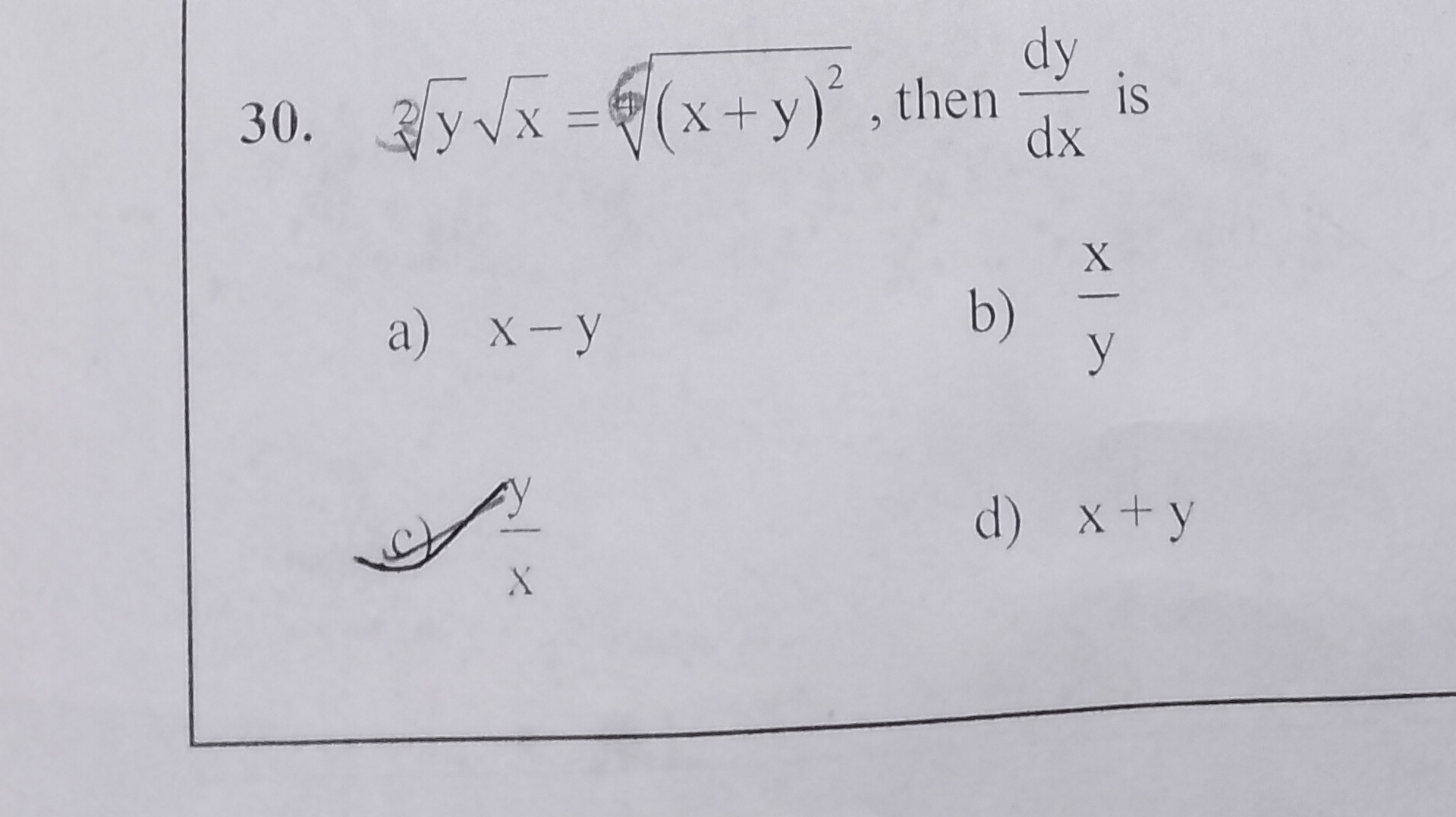
x-y
yx
xy
x+y
2x2y(x−y)
Solution
We start with
3yx=6(x+y)2.A good strategy is to remove the radicals by “raising to a power.” Note that
3yx=(yx)31and
6(x+y)2=((x+y)2)61=(x+y)31.Thus our equation is
(yx)31=(x+y)31.Raising both sides to the power 3 gives
yx=x+y.It is clearer to write the square root as a power:
yx21=x+y.A very neat alternative is to “raise both sides to the 6th power” directly: Since
[(yx)31]6=(yx)2=y2x,and
[(x+y)31]6=(x+y)2,we have
y2x=(x+y)2.Either way (cube‐power or 6th‐power) you get an equivalent relation. (It is easy to check that from yx=x+y one may recover y2x=(x+y)2.)
We now differentiate the equation obtained by the 6th–power method:
y2x=(x+y)2.(1)Differentiate (1) implicitly with respect to x. The left‐side is a product x⋅y2:
dxd[y2x]=y2+2xydxdy.The right–side is:
dxd[(x+y)2]=2(x+y)(1+dxdy).So we have:
y2+2xyy′=2(x+y)(1+y′).Gather the terms containing y′ on one side:
2xyy′−2(x+y)y′=2(x+y)−y2.Factor y′:
y′[2xy−2(x+y)]=2(x+y)−y2.Thus,
y′=2(xy−(x+y))2(x+y)−y2.(2)This answer, although “correct,” can be rewritten in a different form by using the original relation. (In fact, if one had instead raised
yx=x+y,to the proper power and used logarithmic differentiation, one obtains after a few algebraic steps the equivalent answer)
dxdy=2x2y(x−y).Now, before “boxing up” our final answer we compare with the given options:
a) x−y b) yx c) xy d) x+y.
It is a short exercise to check (for example, at x=4 one finds that the relation forces y=4 so that
dxdy=2⋅164(4−4)=0,whereas none of the options a–d gives 0 when x=4,y=4.)
Thus, the correct derivative is
dxdy=2x2y(x−y),which is not equivalent to any of the choices (a)–(d).
Explanation (minimal):
- Write 3yx=(yx)1/3 and 6(x+y)2=(x+y)1/3.
- Equate: (yx)1/3=(x+y)1/3 ⟹ yx=x+y.
- Alternatively, raise both sides to 6: y2x=(x+y)2.
- Differentiate implicitly: LHS: y2+2xyy′, RHS: 2(x+y)(1+y′).
- Solve for y′ to get: y′=2(xy−(x+y))2(x+y)−y2=2x2y(x−y).
- None of the provided options equals this expression.
Answer:
The correct derivative is
so none of the listed options is correct.
