Question
Question: Heat of combustion of $C_{(s)}$, $H_{2(g)}$ and $C_{2}H_{6(g)}$ are $-x_1$, $-x_2$ and $-x_3$ respec...
Heat of combustion of C(s), H2(g) and C2H6(g) are −x1, −x2 and −x3 respectively. Hence heat of formation of C2H6(g) is
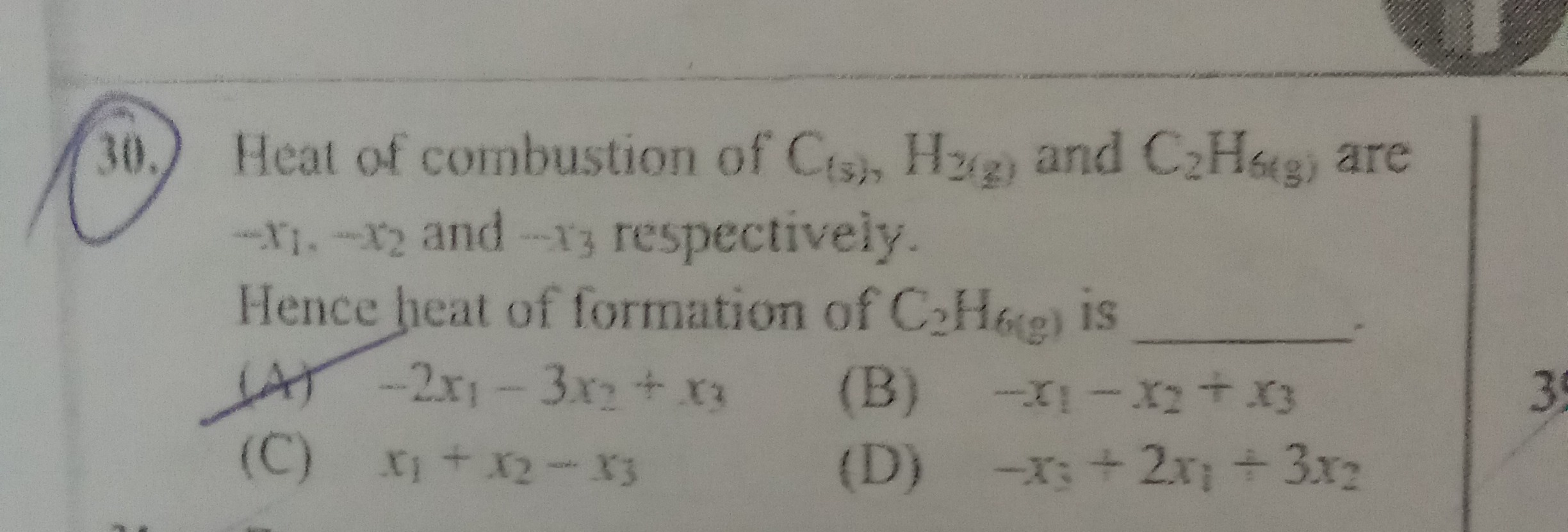
-2x_1 - 3x_2 + x_3
-x_1 - x_2 + x_3
x_1 + x_2 - x_3
-x_3 + 2x_1 + 3x_2
-2x_1 - 3x_2 + x_3
Solution
Write the combustion reaction of ethane:
C2H6+27O2→2CO2+3H2OΔH=−x3.
For the combustion of the elements:
C(s)+O2→CO2ΔH=−x1,
H2(g)+21O2→H2OΔH=−x2.
Thus, formation of combustion products from elements gives:
2CO2:2C(s)+2O2→2CO2ΔH=−2x1,
3H2O:3H2(g)+23O2→3H2OΔH=−3x2.
Combining, formation of the products:
2C(s)+3H2(g)+(2+23)O2→2CO2+3H2OΔH=−2x1−3x2.
Now think of the combustion of ethane as the difference between the formation of products and the formation of ethane (from its elements):
ΔHcomb(C2H6)=[formation of products]−[ΔHf(C2H6)].
That is,
−x3=(−2x1−3x2)−ΔHf(C2H6).
Rearrange to solve for the heat of formation:
ΔHf(C2H6)=−2x1−3x2+x3.
