Question
Question: $\frac{x^3}{\sqrt{x^2 + a^2}}$...
x2+a2x3
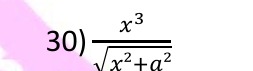
31(x2−2a2)x2+a2+C
Solution
To evaluate the integral ∫x2+a2x3dx, we use the method of substitution.
-
Substitution:
Let u=x2+a2.
Differentiating both sides with respect to x, we get du=2xdx.
From this, we have xdx=21du.
Also, from the substitution, x2=u−a2. -
Rewrite the Integral:
The integral can be written as ∫x2+a2x2⋅xdx.
Substitute x2=u−a2, xdx=21du, and x2+a2=u: ∫u(u−a2)⋅21du -
Simplify and Integrate: 21∫(uu−ua2)du=21∫(u1/2−a2u−1/2)du Now, integrate term by term: 21(1/2+1u1/2+1−a2−1/2+1u−1/2+1)+C 21(3/2u3/2−a21/2u1/2)+C 21(32u3/2−2a2u1/2)+C 31u3/2−a2u1/2+C
-
Substitute Back:
Replace u with x2+a2: 31(x2+a2)3/2−a2(x2+a2)1/2+C -
Factor and Simplify:
Factor out (x2+a2)1/2: (x2+a2)1/2[31(x2+a2)−a2]+C x2+a2[3x2+a2−3a2]+C x2+a2[3x2−2a2]+C 31(x2−2a2)x2+a2+C
