Question

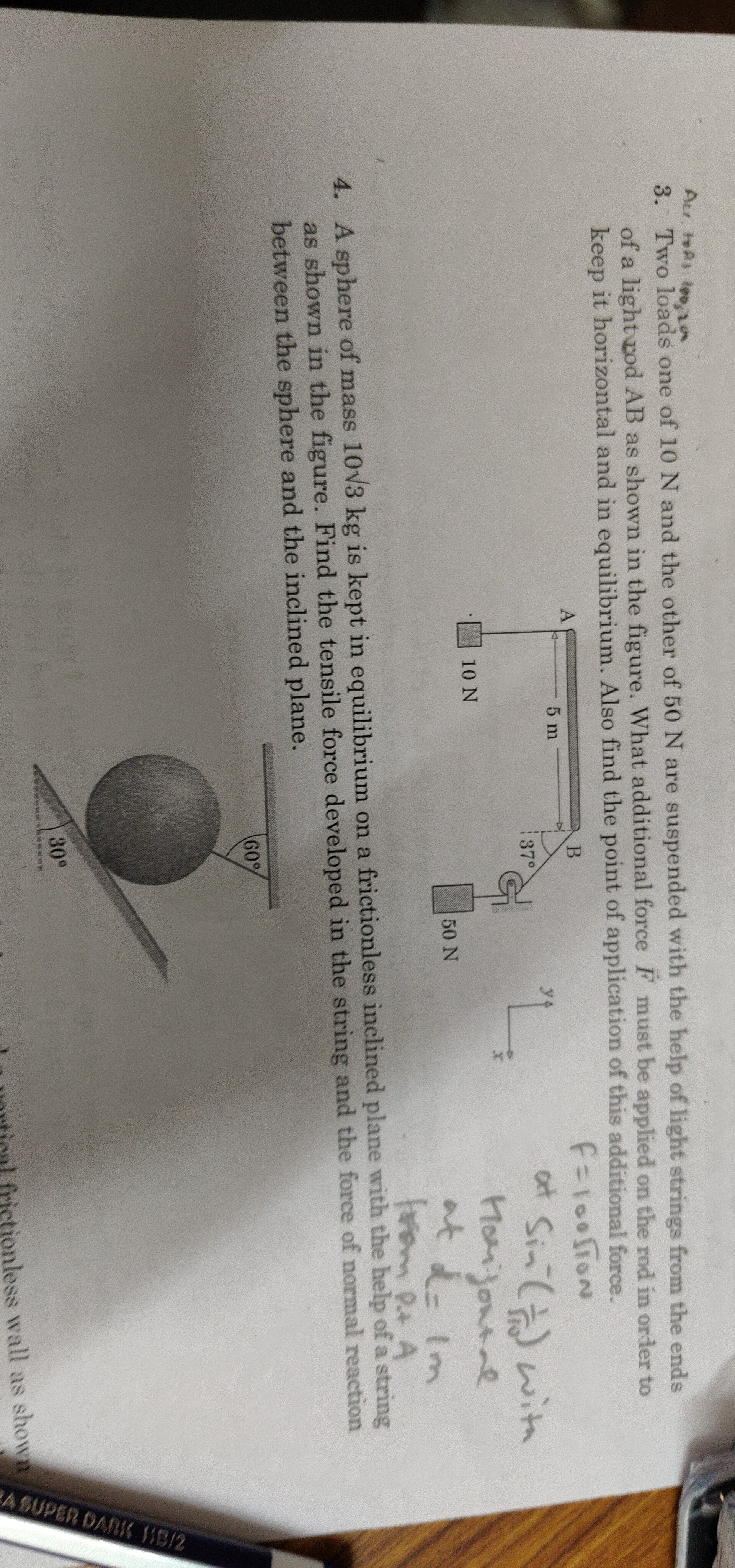
Two loads one of 10 N and the other of 50 N are suspended with the help of light strings from the ends of a light rod AB as shown in the figure. What additional force $\overrightarrow{F}$ must be applied on the rod in order to keep it horizontal and in equilibrium. Also find the point of application of this additional force.

Answer 1

Magnitude: $10\sqrt{34}$ N, Direction: At an angle of $\tan^{-1}(5/3)$ with the horizontal, directed upwards and to the left, Point of application: 4 m from point A.

Answer 2

1. Identify Forces and their Components:
   The rod AB has length 5 m. Let point A be the origin (0,0).

   • Force at A (from 10 N load): $W_A = 10$ N, acting vertically downwards.
   • Force at B (from 50 N load): The string from B passes over a pulley and supports a 50 N load. Thus, the tension in the string is $T_B = 50$ N. The string makes an angle of 37° with the vertical. We resolve this force into horizontal ($F_{Bx}$) and vertical ($F_{By}$) components acting on the rod at B:
     • $F_{Bx} = T_B \sin(37^\circ) = 50 \times (3/5) = 30$ N (acting horizontally to the right).
     • $F_{By} = T_B \cos(37^\circ) = 50 \times (4/5) = 40$ N (acting vertically downwards).
   • Additional Force $\overrightarrow{F}$: Let this force have components $F_x$ and $F_y$, applied at a distance $d$ from point A.

2. Apply Equilibrium Conditions:
   For the rod to be in equilibrium, the net force and net torque must be zero.

   • Sum of Horizontal Forces ($\sum F_x = 0$):
     $F_x + F_{Bx} = 0$
     $F_x + 30 = 0 \implies F_x = -30$ N (acting to the left).

   • Sum of Vertical Forces ($\sum F_y = 0$):
     $F_y - W_A - F_{By} = 0$
     $F_y - 10 - 40 = 0 \implies F_y = 50$ N (acting upwards).

   • Magnitude and Direction of $\overrightarrow{F}$:
     The magnitude of $\overrightarrow{F}$ is:
     $F = \sqrt{F_x^2 + F_y^2} = \sqrt{(-30)^2 + (50)^2} = \sqrt{900 + 2500} = \sqrt{3400} = 10\sqrt{34}$ N.
     The direction of $\overrightarrow{F}$ is given by the angle $\theta$ it makes with the horizontal. Since $F_x$ is negative and $F_y$ is positive, the force is in the second quadrant (upwards and to the left).
     $\tan \theta = \frac{|F_y|}{|F_x|} = \frac{50}{30} = \frac{5}{3}$.
     So, $\theta = \tan^{-1}(5/3)$ with the horizontal (measured counter-clockwise from the positive x-axis, or simply stated as "upwards and to the left").

   • Sum of Torques ($\sum \tau = 0$):
     Let's take moments about point A. Clockwise torques are negative, counter-clockwise are positive.
     The horizontal force $F_{Bx}$ acts along the rod (if the rod is horizontal), so it creates no torque about any point on the rod.

     • Torque due to $W_A = 10$ N at A: $\tau_A = 0$.
     • Torque due to $F_{By} = 40$ N (downwards) at B (distance 5 m from A): $\tau_{By} = -40 \times 5 = -200$ Nm (clockwise).
     • Torque due to $F_y = 50$ N (upwards) at distance $d$ from A: $\tau_{F_y} = +50 \times d$ Nm (counter-clockwise).

   $\sum \tau = 0 \implies 0 - 200 + 50d = 0$
   $50d = 200 \implies d = 4$ m from A.