Question

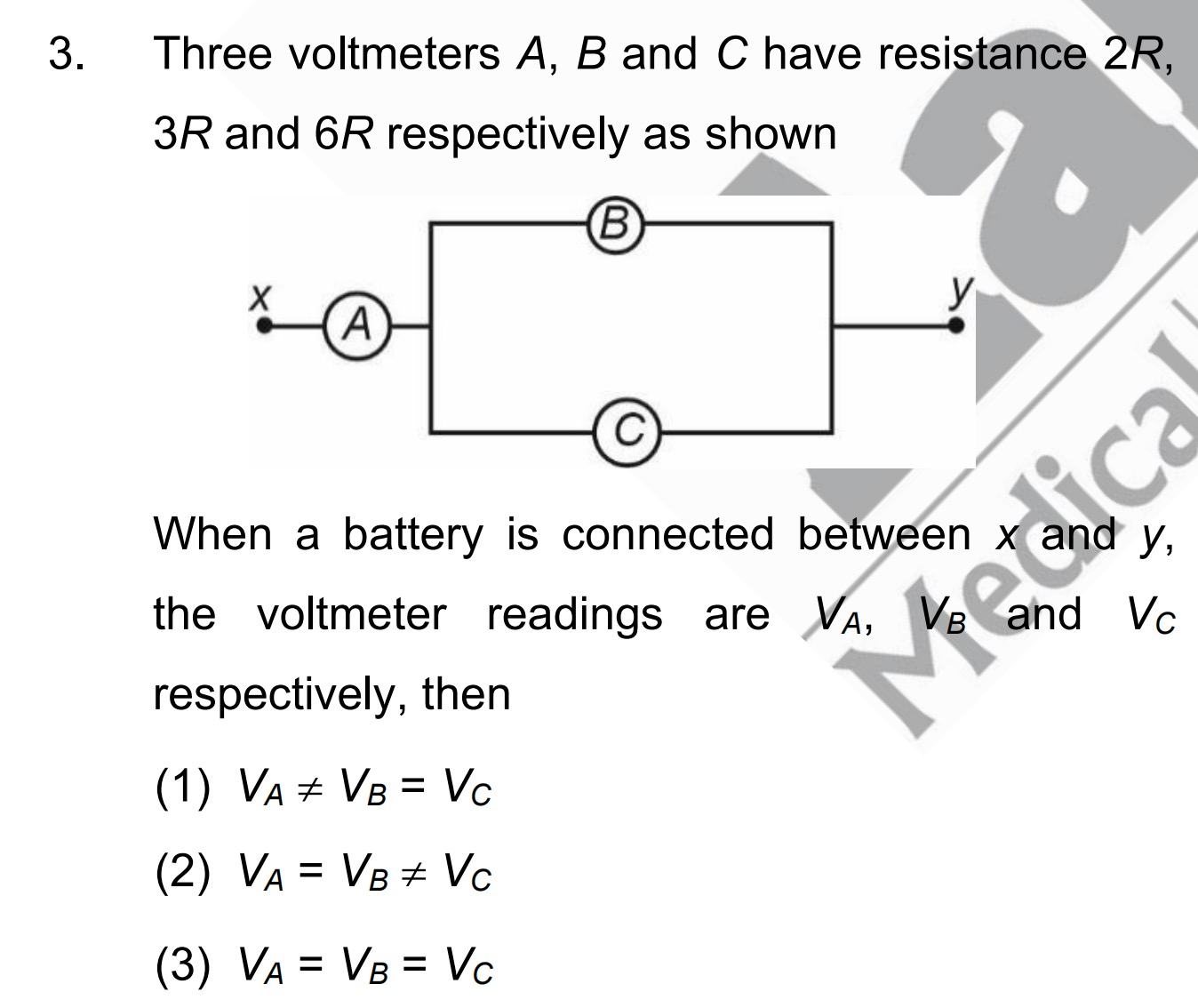
Three voltmeters $A$, $B$ and $C$ have resistance $2R$, $3R$ and $6R$ respectively as shown

When a battery is connected between $x$ and $y$, the voltmeter readings are $V_A$, $V_B$ and $V_C$ respectively, then

• A. $V_A \neq V_B = V_C$
• B. $V_A = V_B \neq V_C$
• C. $V_A = V_B = V_C$

Answer 1

Answer: (C)

$V_A = V_B = V_C$

Answer 2

We start by redrawing the circuit.

Voltmeter B (3R) and Voltmeter C (6R) are in parallel, so the effective resistance is:

$R_{\text{parallel}} = \frac{3R \times 6R}{3R+6R} = \frac{18R^2}{9R} = 2R$

Voltmeter A (2R) is in series with the parallel combination (2R):

$R_{\text{total}} = 2R + 2R = 4R$

Let the battery voltage be $V$.

• The total current:

$I = \frac{V}{4R}$

• Voltage drop across Voltmeter A:

$V_A = I \times 2R = \frac{V}{4R} \times 2R = \frac{V}{2}$

• Voltage drop across the parallel branch, which is the reading for both B and C:

$V_{B}=V_{C} = \frac{V}{2}$

Thus, we have:

$V_A = V_B = V_C$

The parallel combination of voltmeters B (3R) and C (6R) gives an equivalent resistance of $2R$. When connected in series with voltmeter A (2R), the circuit becomes two equal resistances. Therefore, by voltage division, each voltmeter shows half of the battery voltage.