Question
Question: The weight of $1 \times 10^{22}$ molecules of $CuSO_4.5H_2O$ is ......................
The weight of 1×1022 molecules of CuSO4.5H2O is ...................
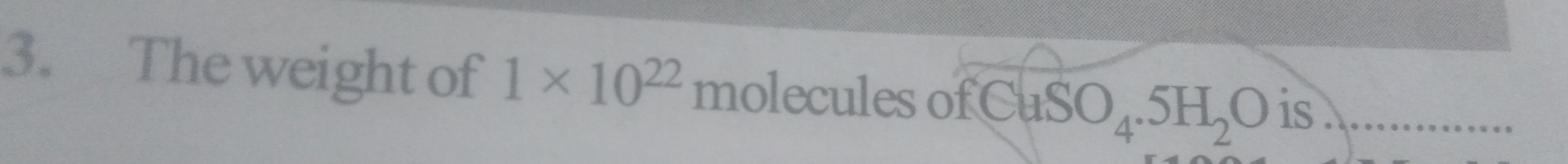
4.144 g
Solution
To find the weight of 1×1022 molecules of CuSO4.5H2O, we need to follow these steps:
-
Calculate the molar mass of CuSO4.5H2O:
We use the standard atomic masses:
Cu = 63.5 g/mol
S = 32.0 g/mol
O = 16.0 g/mol
H = 1.0 g/molMolar mass of CuSO4 = M(Cu) + M(S) + 4 * M(O) = 63.5 + 32.0 + 4 * 16.0 = 63.5 + 32.0 + 64.0 = 159.5 g/mol.
Molar mass of H2O = 2 * M(H) + M(O) = 2 * 1.0 + 16.0 = 2.0 + 16.0 = 18.0 g/mol.
Molar mass of 5H2O = 5 * M(H2O) = 5 * 18.0 = 90.0 g/mol.Molar mass of CuSO4.5H2O = M(CuSO4) + M(5H2O) = 159.5 + 90.0 = 249.5 g/mol.
-
Determine the number of moles:
We are given the number of molecules as 1×1022.
Avogadro's number (NA) is 6.022×1023 molecules/mol.Number of moles = (Number of molecules) / (NA)
Number of moles = (1×1022)/(6.022×1023) mol
Number of moles = (1/6.022)×10(22−23) mol
Number of moles = (1/6.022)×10−1 mol -
Calculate the weight (mass):
Weight = Number of moles * Molar mass
Weight = ((1/6.022)×10−1 mol)×(249.5 g/mol)
Weight = (249.5/6.022)×10−1 gLet's calculate the value:
249.5/6.022≈41.4397Weight ≈41.4397×10−1 g
Weight ≈4.14397 g
Given the number of molecules 1×1022, if interpreted as having 2 significant figures (1.0×1022), and using NA with 4 significant figures (6.022×1023) and Molar Mass with 4 significant figures (249.5), the result should be reported with 2 significant figures, which would be 4.1 g. However, in such problems, it is common practice to use the standard constants and report the result with a precision consistent with those constants (usually 3-4 significant figures) unless the input number clearly limits the precision to fewer significant figures. Assuming at least 3 significant figures are expected.
Using the calculated value ≈4.14397 g.
Rounding to 3 significant figures gives 4.14 g.
Rounding to 4 significant figures gives 4.144 g.
Let's provide the answer with 3 decimal places for sufficient precision.
The weight is approximately 4.144 g.
