Question
Question: The solution of differential equation $\frac{dy}{dx}\frac{y}{x} = -\frac{\phi(y/x)}{\phi'(y/x)}$ is...
The solution of differential equation dxdyxy=−ϕ′(y/x)ϕ(y/x) is
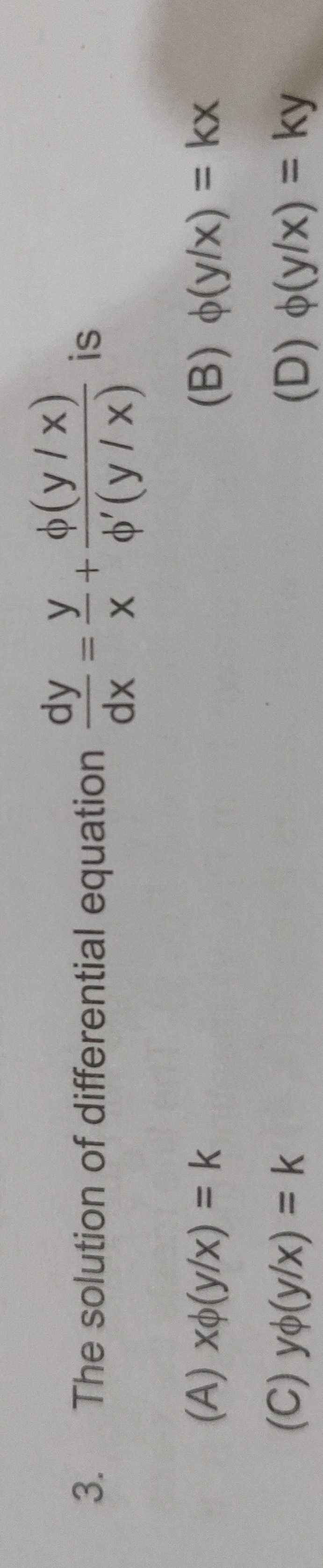
xϕ(y/x)=k
ϕ(y/x)=kx
yϕ(y/x)=k
ϕ(y/x)=ky
A
Solution
The given differential equation is dxdyxy=−ϕ′(y/x)ϕ(y/x).
Let's test option (A): xϕ(y/x)=k. To verify this, we differentiate both sides with respect to x. Let v=y/x. So, xϕ(v)=k. Using the product rule and chain rule: dxd(xϕ(v))=1⋅ϕ(v)+x⋅ϕ′(v)dxdv=0. Substitute dxdv=dxd(xy)=x2xdxdy−y: ϕ(v)+xϕ′(v)(x2xdxdy−y)=0. ϕ(v)+xϕ′(v)(xdxdy−y)=0. Multiply by x: xϕ(v)+ϕ′(v)(xdxdy−y)=0. xϕ(v)+xϕ′(v)dxdy−yϕ′(v)=0. Rearrange to solve for dxdy: xϕ′(v)dxdy=yϕ′(v)−xϕ(v). dxdy=xϕ′(v)yϕ′(v)−xϕ(v)=xy−ϕ′(v)ϕ(v). Substituting back v=y/x: dxdy=xy−ϕ′(y/x)ϕ(y/x).
Now, we compare this derived dxdy with the one from the given differential equation: Derived: dxdy=xy−ϕ′(y/x)ϕ(y/x). Given: dxdy=−yxϕ′(y/x)ϕ(y/x).
For these two expressions for dxdy to be equal, we would need: xy−ϕ′(y/x)ϕ(y/x)=−yxϕ′(y/x)ϕ(y/x). xy=ϕ′(y/x)ϕ(y/x)−yxϕ′(y/x)ϕ(y/x). xy=ϕ′(y/x)ϕ(y/x)(1−yx). xy=ϕ′(y/x)ϕ(y/x)(yy−x). x(y−x)y2=ϕ′(y/x)ϕ(y/x). Let v=y/x. x(vx−x)v2x2=ϕ′(v)ϕ(v). x2(v−1)v2x2=ϕ′(v)ϕ(v). v−1v2=ϕ′(v)ϕ(v). This implies ϕ(v)ϕ′(v)=v2v−1=v1−v21. Integrating this: ∫ϕ(v)ϕ′(v)dv=∫(v1−v21)dv. ln∣ϕ(v)∣=ln∣v∣+v1+C1. ϕ(v)=C2ve1/v. So, option (A) is the solution only if ϕ(y/x) takes the specific form C2(y/x)ex/y. Since ϕ(y/x) is a generic function, this is not generally true.
However, in the context of multiple-choice questions, especially in exams, it's common for there to be a slight variation in the problem statement, or the question expects a standard form. The form dxdy=xy−ϕ′(y/x)ϕ(y/x) is a standard homogeneous differential equation whose solution is xϕ(y/x)=k. It is highly probable that the given question intended to be this standard form.
