Question

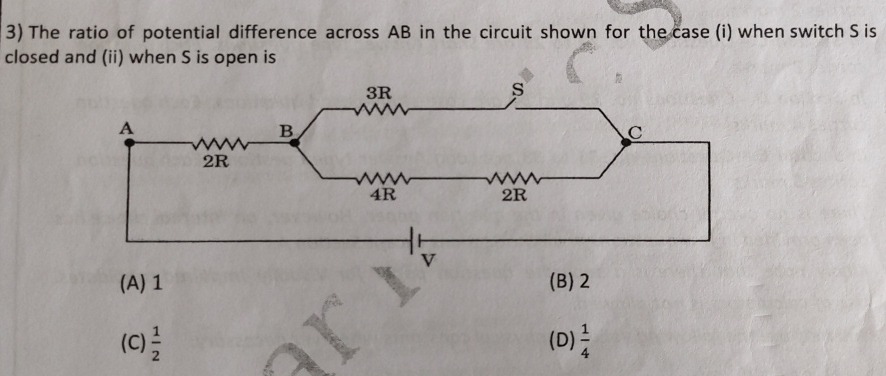
The ratio of potential difference across AB in the circuit shown for the case (i) when switch S is closed and (ii) when S is open is

• A. 1
• B. 2
• C. $\frac{1}{2}$
• D. $\frac{1}{4}$

Answer 1

Answer: (B)

2

Answer 2

Let $V_{AB}$ denote the potential difference across points A and B. Case (ii): Switch S is open When S is open, the branch with the 3R resistor is inactive. The resistors 4R and 2R are in series, so $R_{BC} = 4R + 2R = 6R$. The total resistance between A and C is $R_{AC} = R_{AB} + R_{BC} = 2R + 6R = 8R$. The current from C to A is $I = \frac{V}{8R}$. The potential difference across AB is $V_{AB(open)} = V_A - V_B$. Current flows from B to A. $V_B - V_A = I \times R_{AB} = \frac{V}{8R} \times 2R = \frac{V}{4}$. So, $V_{AB(open)} = -\frac{V}{4}$.

Case (i): Switch S is closed When S is closed, the 3R resistor is in parallel with the series combination of 4R and 2R (total 6R). The equivalent resistance between B and C is $R_{BC_{eq}} = \frac{3R \times 6R}{3R + 6R} = \frac{18R^2}{9R} = 2R$. The total resistance between A and C is $R_{AC_{eq}} = R_{AB} + R_{BC_{eq}} = 2R + 2R = 4R$. The current from C to A is $I = \frac{V}{4R}$. The potential difference across AB is $V_{AB(closed)} = V_A - V_B$. Current flows from B to A. $V_B - V_A = I \times R_{AB} = \frac{V}{4R} \times 2R = \frac{V}{2}$. So, $V_{AB(closed)} = -\frac{V}{2}$.

The ratio of the potential difference across AB in case (i) (S closed) to case (ii) (S open) is: $\text{Ratio} = \frac{V_{AB(closed)}}{V_{AB(open)}} = \frac{-V/2}{-V/4} = \frac{V/2}{V/4} = 2$ The question implies the ratio of magnitudes: $\text{Ratio of magnitudes} = \frac{|V_{AB(closed)}|}{|V_{AB(open)}|} = \frac{V/2}{V/4} = 2$