Question

The output of an AC generator is given by: $E = E_m \sin \left( \omega t - \frac{\pi}{4} \right)$ and current is given by $i = i_m \sin \left( \omega t - \frac{3\pi}{4} \right)$. The circuit contains a single

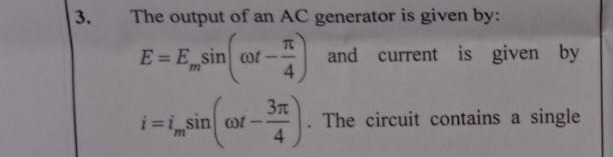
Answer 1

inductor

Answer 2

The phase difference between voltage $E = E_m \sin(\omega t + \phi_E)$ and current $i = i_m \sin(\omega t + \phi_i)$ is $\Delta \phi = \phi_E - \phi_i$. Given $E = E_m \sin \left( \omega t - \frac{\pi}{4} \right)$ and $i = i_m \sin \left( \omega t - \frac{3\pi}{4} \right)$. $\Delta \phi = \left( -\frac{\pi}{4} \right) - \left( -\frac{3\pi}{4} \right) = -\frac{\pi}{4} + \frac{3\pi}{4} = \frac{2\pi}{4} = \frac{\pi}{2}$. A positive phase difference means voltage leads current. When voltage leads current by $\frac{\pi}{2}$, the circuit contains an inductor.