Question

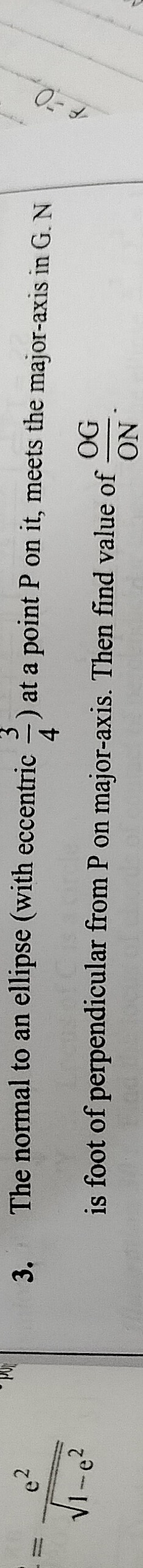
The normal to an ellipse (with eccentric $\frac{3}{4}$) at a point P on it, meets the major-axis in G. N is foot of perpendicular from P on major-axis. Then find value of $\frac{OG}{ON}$.

• A. $\frac{9}{16}$
• B. $\frac{16}{9}$
• C. $\frac{3}{4}$
• D. $\frac{4}{3}$

Answer 1

Answer: (A)

$\frac{9}{16}$

Answer 2

Let the ellipse be $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. For a point P$(x_1, y_1)$ on the ellipse, N is the foot of the perpendicular to the major axis, so N is $(x_1, 0)$ and ON = $|x_1|$. The normal to the ellipse at P is $\frac{a^2x}{x_1} - \frac{b^2y}{y_1} = a^2 - b^2$. When the normal meets the major axis (y=0), we get $\frac{a^2x_G}{x_1} = a^2 - b^2$, so $x_G = x_1 \frac{a^2 - b^2}{a^2} = x_1 \left(1 - \frac{b^2}{a^2}\right)$. Since $e^2 = 1 - \frac{b^2}{a^2}$, we have $x_G = x_1 e^2$. Thus, OG = $|x_1 e^2|$. The ratio $\frac{OG}{ON} = \frac{|x_1 e^2|}{|x_1|} = e^2$. Given $e = \frac{3}{4}$, $\frac{OG}{ON} = \left(\frac{3}{4}\right)^2 = \frac{9}{16}$.