Question

The moment of inertia of a solid cylinder about an axis parallel to its length and passing through its centre is equal to its moment of inertia about an axis perpendicular to the length of cylinder and passing through its centre. The ratio of radius of cylinder and its length is:

• A. 1:$\sqrt{2}$
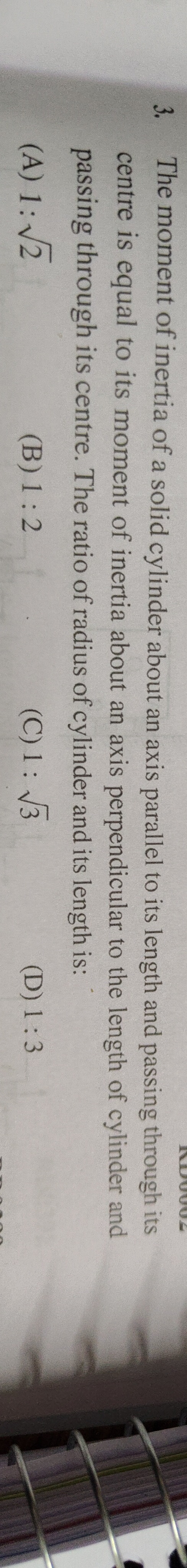
• B. 1:2
• C. 1:$\sqrt{3}$
• D. 1:3

Answer 1

Answer: (C)

1:$\sqrt{3}$

Answer 2

Let $M$ be the mass of the solid cylinder, $R$ be its radius, and $L$ be its length.

1. Moment of inertia about an axis parallel to its length and passing through its centre ($I_1$): $I_1 = \frac{1}{2}MR^2$

2. Moment of inertia about an axis perpendicular to the length of the cylinder and passing through its centre ($I_2$): $I_2 = M\left(\frac{L^2}{12} + \frac{R^2}{4}\right)$

According to the problem statement, these two moments of inertia are equal: $I_1 = I_2$ $\frac{1}{2}MR^2 = M\left(\frac{L^2}{12} + \frac{R^2}{4}\right)$

We can cancel out the mass $M$ from both sides of the equation: $\frac{1}{2}R^2 = \frac{L^2}{12} + \frac{R^2}{4}$

Now, we need to solve for the ratio $R:L$. Let's rearrange the terms to group $R^2$ terms: $\frac{1}{2}R^2 - \frac{1}{4}R^2 = \frac{L^2}{12}$ $\frac{1}{4}R^2 = \frac{L^2}{12}$

Now, we want to find the ratio $R/L$. Let's isolate $R^2/L^2$: $3R^2 = L^2$ $\frac{R^2}{L^2} = \frac{1}{3}$

Take the square root of both sides: $\frac{R}{L} = \sqrt{\frac{1}{3}}$ $\frac{R}{L} = \frac{1}{\sqrt{3}}$

Thus, the ratio of the radius of the cylinder to its length is $1:\sqrt{3}$.