Question
Question: The velocity (v) and time (t) graph of a body in a straight line motion is shown in the figure. The ...
The velocity (v) and time (t) graph of a body in a straight line motion is shown in the figure. The point S is at 4.333 seconds. The total distance covered by the body in 6s is :
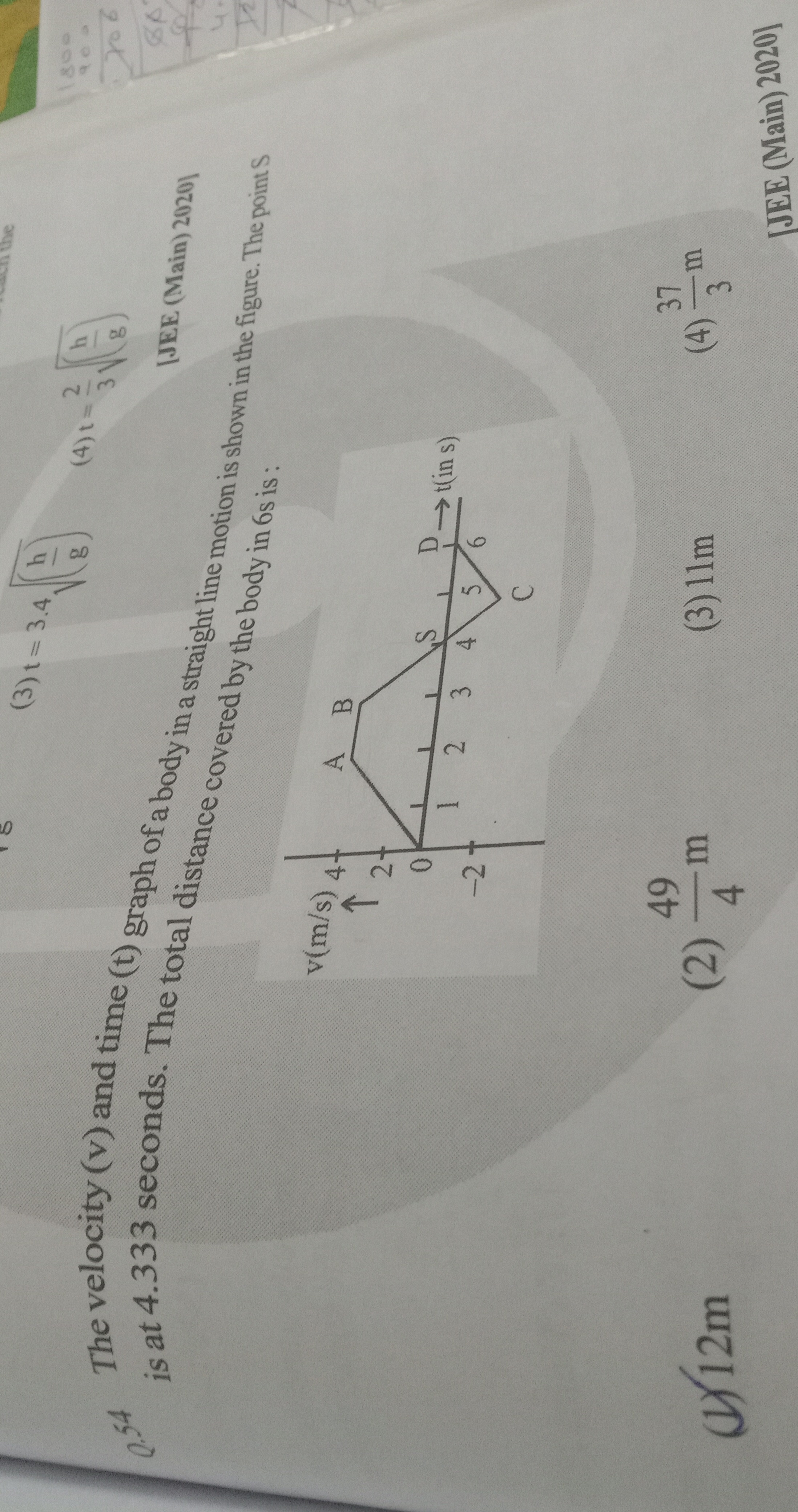
449m
11m
337m
337m
Solution
The problem asks for the total distance covered by a body in 6 seconds, given its velocity-time (v-t) graph. The total distance covered is the sum of the magnitudes of the areas under the v-t graph.
Let's break down the graph into distinct segments and calculate the area for each:
-
Segment O to A (t = 0s to t = 2s):
- This segment represents the motion from (0,0) to (2,4).
- The shape formed with the time axis is a triangle.
- Base of the triangle = 2s.
- Height of the triangle = 4 m/s.
- Area (Distance) for this segment = 21×base×height=21×2s×4 m/s=4 m.
-
Segment A to B (t = 2s to t = 3s):
- This segment represents the motion from (2,4) to (3,4).
- The shape formed with the time axis is a rectangle.
- Base of the rectangle = 3s - 2s = 1s.
- Height of the rectangle = 4 m/s.
- Area (Distance) for this segment = base×height=1s×4 m/s=4 m.
-
Segment B to D (t = 3s to t = 6s):
-
This segment goes from (3,4) to (6,-2).
-
The problem states that point S is at 4.333 seconds. We recognize 4.333 seconds as 431 s=313 s.
-
The point S is where the velocity becomes zero. So, the line segment from B to D crosses the time axis at t=313 s. This implies that the motion changes direction at t=313 s.
-
We need to calculate the area for two sub-segments: B to S (above the axis) and S to D (below the axis).
-
Sub-segment B to S (t = 3s to t = 13/3 s):
- This forms a triangle above the time axis.
- Base of the triangle = 313 s−3 s=313−9 s=34 s.
- Height of the triangle (velocity at t=3s) = 4 m/s.
- Area (Distance) for this segment = 21×base×height=21×34 s×4 m/s=616 m=38 m.
-
Sub-segment S to D (t = 13/3 s to t = 6s):
- This forms a triangle below the time axis.
- Base of the triangle = 6 s−313 s=318−13 s=35 s.
- Magnitude of Height (velocity at t=6s) = ∣−2 m/s∣=2 m/s.
- Area (Distance) for this segment = 21×base×height=21×35 s×2 m/s=35 m.
-
Total Distance Covered:
Sum the areas (distances) from all segments: Total Distance = (Distance O to A) + (Distance A to B) + (Distance B to S) + (Distance S to D) Total Distance = 4 m+4 m+38 m+35 m Total Distance = 8 m+38+5 m Total Distance = 8 m+313 m Total Distance = 324 m+313 m Total Distance = 337 m.
The final answer is 337m.
Explanation of the solution: The total distance covered by the body is the sum of the magnitudes of the areas under the velocity-time graph.
- Calculate the area of the triangle from t=0s to t=2s: 21×2×4=4 m.
- Calculate the area of the rectangle from t=2s to t=3s: 1×4=4 m.
- The point S where velocity is zero is given as t = 4.333s = 13/3 s.
- Calculate the area of the triangle from t=3s to t=13/3s (above axis): 21×(313−3)×4=21×34×4=38 m.
- Calculate the area of the triangle from t=13/3s to t=6s (below axis, take magnitude): 21×(6−313)×∣−2∣=21×35×2=35 m.
- Sum all the distances: 4+4+38+35=8+313=324+13=337 m.
