Question

3 resistors $3\Omega ,4\Omega$ and $6\Omega$ are connected in a parallel combination and are connected to a cell of 2V and internal resistance $\dfrac{2}{3}\Omega$. Find the current drawn from the cell and also, current through $3\Omega$ resistance.

Answer 1

When a cell with an emf E and internal resistance r is connected to an external resistance R, the actual voltage realised on the external resistance is lesser than the emf. This voltage is called terminal voltage and the current that flows through the circuit is called terminal current.
The terminal (main branch) current is given by the formula:
$I = \dfrac{E}{{R + r}}$
where E = emf, r = internal resistance and R = net resistance in the circuit.

Complete step by step answer:
Consider 3 resistors of values $3\Omega ,4\Omega \& 6\Omega$ connected in a parallel combination to a cell of emf 2V or internal resistance $r = \dfrac{2}{3}\Omega$.

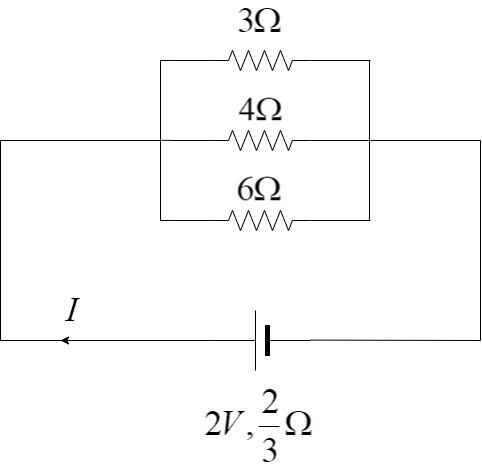
The net resistance offered by the parallel combination,
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{3} + \dfrac{1}{4} + \dfrac{1}{6}$
$\Rightarrow \dfrac{1}{R} = \dfrac{{4 + 3 + 2}}{{12}}$
$\Rightarrow \dfrac{1}{R} = \dfrac{9}{{12}}$
$\Rightarrow R = \dfrac{{12}}{9} = \dfrac{4}{3}\Omega$
The terminal current in the circuit is given by the formula –
$I = \dfrac{E}{{R + r}}$
Emf, $E = 2V$
Internal resistance, $r = \dfrac{2}{3}\Omega$
Substituting the values, we get –
$I = \dfrac{2}{{\dfrac{4}{3} + \dfrac{2}{3}}}$
$\Rightarrow I = \dfrac{{2 \times 3}}{6}$
$\Rightarrow I = \dfrac{6}{6} = 1A$
Hence, the main current in the circuit is equal to 1A.
To find the current through the $3\Omega$ resistor, it is important to find the voltage drop across the parallel combination and this voltage must be divided by the resistance to obtain the branch current through the resistor. The voltage drop across the parallel combination can be computed by multiplying the main current with the net resistance of the parallel combination.
Voltage across the parallel combination, ${V_P} = IR = 1 \times \dfrac{4}{3} = \dfrac{4}{3}V$
Current through the $3\Omega$ resistor, ${I_3} = \dfrac{{{V_P}}}{{3\Omega }}$
$\Rightarrow {I_3} = \dfrac{{\dfrac{4}{3}}}{3} = \dfrac{4}{{3 \times 3}} = \dfrac{4}{9} = 0.44A$
Thus, the current through the $3\Omega$ resistor, ${I_3} = 0.44A$.

Note: The voltage available in the circuit, will always be lesser than the emf because of the internal resistance. Hence, the terminal voltage V is always lesser than the emf E. If, in any scenario, we obtain the terminal voltage greater than the emf E, it is evident that you are on the wrong path to the solution and you should check the steps again.