Question

Number of positive integral solutions of the equation $\frac{1}{x}+\frac{2}{y}=\frac{1}{4}$:

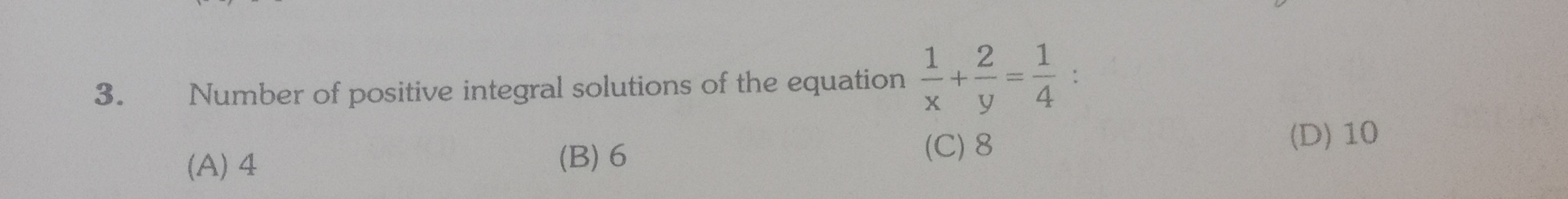
• A. 4
• B. 6
• C. 8
• D. 10

Answer 1

Answer: (B)

6

Answer 2

The equation can be rewritten as $(x-4)(y-8) = 32$. Since $x$ and $y$ must be positive integers, $x > 4$, which implies $x-4 \ge 1$. Thus, $x-4$ must be a positive divisor of 32. The number of positive divisors of $32 = 2^5$ is $5+1=6$. Each positive divisor of 32 for $x-4$ corresponds to a unique positive integer solution for $(x,y)$.