Question
Question: Mole fraction of aqueous solution of $CH_3COOH$ is 0.1. Select incorrect statement -...
Mole fraction of aqueous solution of CH3COOH is 0.1. Select incorrect statement -
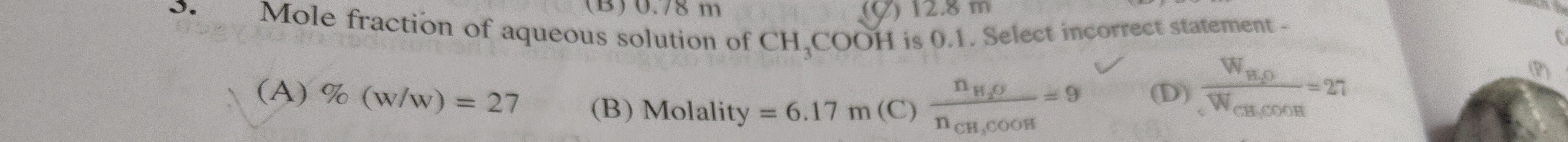
%(w/w) = 27
Molality = 6.17 m
nCH3COOHnH2O=9
WCH3COOHWH2O=27
D
Solution
The problem asks us to identify the incorrect statement regarding an aqueous solution of CH3COOH where its mole fraction is 0.1.
Let XCH3COOH be the mole fraction of CH3COOH and XH2O be the mole fraction of H2O. Given: XCH3COOH=0.1. Since it's an aqueous solution, the only other component is water. The sum of mole fractions in a solution is 1. XCH3COOH+XH2O=1 0.1+XH2O=1 XH2O=0.9
We know that mole fraction is defined as Xi=ntotalni. So, nCH3COOH+nH2OnCH3COOH=0.1 and nCH3COOH+nH2OnH2O=0.9.
Let's check each option:
Option (C): nCH3COOHnH2O=9 Divide the mole fraction of H2O by the mole fraction of CH3COOH: XCH3COOHXH2O=nCH3COOH/(nCH3COOH+nH2O)nH2O/(nCH3COOH+nH2O)=nCH3COOHnH2O nCH3COOHnH2O=0.10.9=9. So, statement (C) is correct.
To evaluate other options, let's assume a basis for calculation. Let nCH3COOH=1 mole. From nCH3COOHnH2O=9, we get nH2O=9×1=9 moles.
Now, calculate the masses of CH3COOH and H2O. Molar mass of CH3COOH: C=12, H=1, O=16 MCH3COOH=(2×12)+(4×1)+(2×16)=24+4+32=60 g/mol. Molar mass of H2O: H=1, O=16 MH2O=(2×1)+16=18 g/mol.
Mass of CH3COOH(WCH3COOH)=nCH3COOH×MCH3COOH=1 mol×60 g/mol=60 g. Mass of H2O(WH2O)=nH2O×MH2O=9 mol×18 g/mol=162 g.
Option (A): % (w/w) = 27 Percentage by weight (% w/w) of CH3COOH=Total mass of solutionMass of CH3COOH×100 Total mass of solution = WCH3COOH+WH2O=60 g+162 g=222 g. % (w/w) = 222 g60 g×100=2226000≈27.027%. Rounding to the nearest integer, it is 27. So, statement (A) is correct.
Option (B): Molality = 6.17 m Molality (m) is defined as moles of solute per kilogram of solvent. Solute: CH3COOH, Solvent: H2O. Moles of solute (nCH3COOH) = 1 mole. Mass of solvent (WH2O) = 162 g = 0.162 kg. Molality (m) = WH2O (in kg)nCH3COOH=0.162 kg1 mol≈6.1728 m. Rounding to two decimal places, it is 6.17 m. So, statement (B) is correct.
Option (D): WCH3COOHWH2O=27 Using the calculated masses: WCH3COOHWH2O=60 g162 g=60162=1027=2.7. The statement claims the ratio is 27. So, statement (D) is incorrect.
The question asks to select the incorrect statement.
The final answer is D
Explanation of the solution:
- From the mole fraction of CH3COOH (0.1), determine the mole fraction of H2O (0.9).
- Calculate the ratio of moles of H2O to CH3COOH: nCH3COOHnH2O=0.10.9=9. This confirms option (C) is correct.
- Assume 1 mole of CH3COOH. Then, moles of H2O are 9 moles.
- Calculate the masses: WCH3COOH=1 mol×60 g/mol=60 g. WH2O=9 mol×18 g/mol=162 g.
- Calculate % (w/w) of CH3COOH: 60+16260×100=22260×100≈27.03%. This confirms option (A) is correct.
- Calculate molality: m=0.162 kg1 mol≈6.17 m. This confirms option (B) is correct.
- Calculate the ratio of masses: WCH3COOHWH2O=60162=2.7. This contradicts option (D) which states the ratio is 27. Therefore, statement (D) is incorrect.
