Question
Question: $\lim_{x \leftarrow 0} \frac{x^2}{sin(x^2)cos(x)}$...
limx←0sin(x2)cos(x)x2
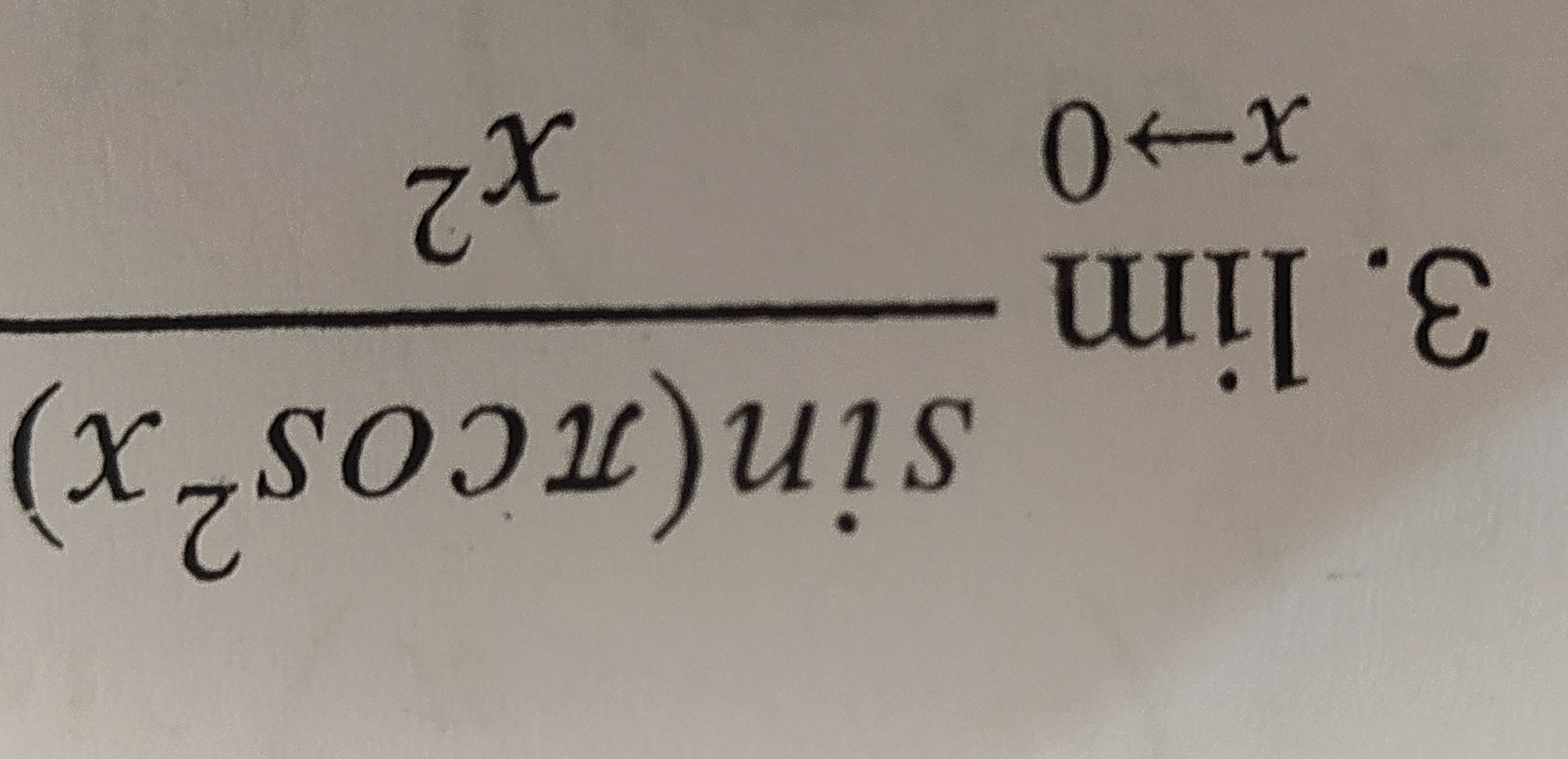
Answer
1
Explanation
Solution
The limit is of the form 0/0. Rewrite the expression as a product sin(x2)x2⋅cos(x)1. Use the standard limit limy→0sin(y)y=1 for the first term by substituting y=x2. Evaluate the limit of the second term cos(x)1 by direct substitution as x→0. The limit of the product is the product of the limits.
