Question

Let there be exactly three chords of $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, a>b>0$ which are passing through point $(a,0)$ are bisected by the parabola $y^2 = 4ax$. Then

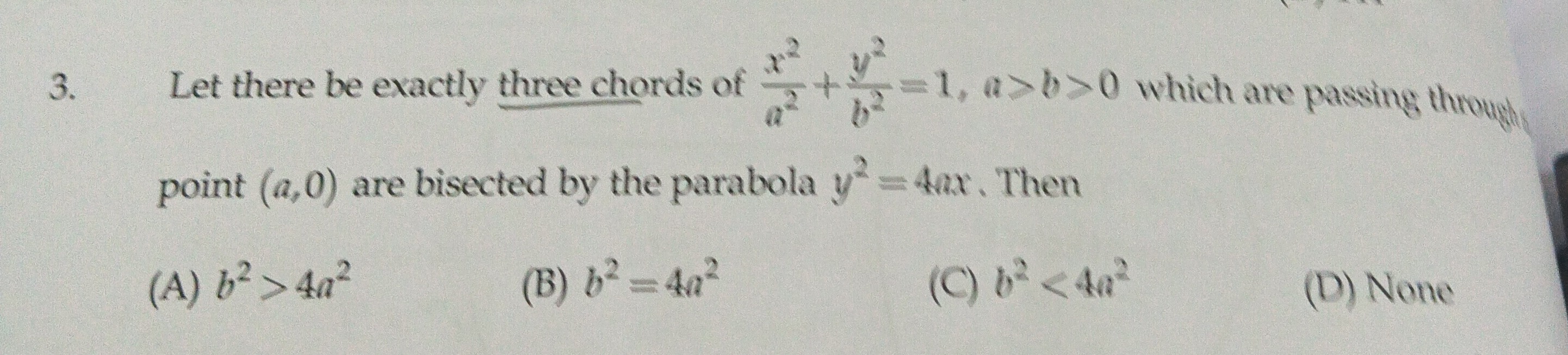
• A. $b^2 > 4a^2$
• B. $b^2 = 4a^2$
• C. $b^2 < 4a^2$
• D. None

Answer 1

Answer: (A)

$b^2 > 4a^2$

Answer 2

Let the equation of the ellipse be $E: \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, $a>b>0$.
Let the equation of the parabola be $P: y^2 = 4ax$.
Let $A$ be the point $(a,0)$.
Let $M(x_1, y_1)$ be the midpoint of a chord of the ellipse passing through $A(a,0)$.

The equation of a chord of the ellipse with midpoint $(x_1, y_1)$ is given by $T=S_1$, where $T = \frac{xx_1}{a^2} + \frac{yy_1}{b^2} - 1$ and $S_1 = \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2} - 1$.
The equation of the chord is $\frac{xx_1}{a^2} + \frac{yy_1}{b^2} = \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2}$.
Since the chord passes through $A(a,0)$, we substitute $(x,y)=(a,0)$ into the equation:
$\frac{a x_1}{a^2} + \frac{0 \cdot y_1}{b^2} = \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2}$
$\frac{x_1}{a} = \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2}$
Multiplying by $a^2 b^2$, we get $ab^2 x_1 = b^2 x_1^2 + a^2 y_1^2$, which can be rearranged as:
$b^2 x_1^2 - ab^2 x_1 + a^2 y_1^2 = 0 \quad (*)$

The problem states that these chords are bisected by the parabola $y^2 = 4ax$. This means the midpoint $(x_1, y_1)$ of such a chord lies on the parabola. So, $(x_1, y_1)$ must satisfy:
$y_1^2 = 4ax_1 \quad (**)$

We are looking for the number of points $(x_1, y_1)$ that satisfy both equations $(*)$ and $(**)$.
Substitute $y_1^2 = 4ax_1$ from $(**)$ into $(*)$:
$b^2 x_1^2 - ab^2 x_1 + a^2 (4ax_1) = 0$
$b^2 x_1^2 - ab^2 x_1 + 4a^3 x_1 = 0$
Factor out $x_1$:
$x_1 (b^2 x_1 - ab^2 + 4a^3) = 0$

This equation yields two possibilities for $x_1$:

1. $x_1 = 0$
   If $x_1 = 0$, then from $y_1^2 = 4ax_1$, we get $y_1^2 = 4a(0) = 0$, so $y_1 = 0$.
   This gives the midpoint $(x_1, y_1) = (0,0)$.
   The point $(0,0)$ is the midpoint of the major axis of the ellipse, which is the chord connecting $(-a,0)$ and $(a,0)$. This chord passes through $(a,0)$. The midpoint $(0,0)$ lies on the parabola $y^2=4ax$ since $0^2 = 4a(0)$. So, $(0,0)$ is a valid midpoint. This corresponds to one chord.

2. $b^2 x_1 - ab^2 + 4a^3 = 0$
   $b^2 x_1 = ab^2 - 4a^3$
   $x_1 = \frac{ab^2 - 4a^3}{b^2} = a - \frac{4a^3}{b^2}$
   Let this value be $x_{1, \text{new}} = a - \frac{4a^3}{b^2}$.
   Substitute this value of $x_1$ into $y_1^2 = 4ax_1$:
   $y_1^2 = 4a \left( a - \frac{4a^3}{b^2} \right) = 4a^2 \left( 1 - \frac{4a^2}{b^2} \right) = \frac{4a^2}{b^2} (b^2 - 4a^2)$

For $y_1$ to be a real number, $y_1^2$ must be non-negative. Since $\frac{4a^2}{b^2} > 0$ (as $a, b > 0$), we must have $b^2 - 4a^2 \ge 0$, which means $b^2 \ge 4a^2$.

We are given that there are exactly three chords passing through $(a,0)$ that are bisected by the parabola. This means there must be exactly three distinct midpoints $(x_1, y_1)$ satisfying both equations.

From the analysis above:

• The case $x_1=0$ gives the midpoint $(0,0)$. This is always one solution.
• The case $b^2 x_1 - ab^2 + 4a^3 = 0$ gives $x_1 = a - \frac{4a^3}{b^2}$.

If $b^2 = 4a^2$, then $x_{1, \text{new}} = a - \frac{4a^3}{4a^2} = a - a = 0$.
$y_1^2 = \frac{4a^2}{4a^2} (4a^2 - 4a^2) = 0$.
This gives $x_1 = 0, y_1 = 0$, which is the same midpoint $(0,0)$ we already found.
So, if $b^2 = 4a^2$, there is only one midpoint $(0,0)$, corresponding to only one chord. This contradicts the condition of exactly three chords.

If $b^2 < 4a^2$, then $b^2 - 4a^2 < 0$.
$y_1^2 = \frac{4a^2}{b^2} (b^2 - 4a^2) < 0$.
Since $y_1^2$ must be non-negative for $y_1$ to be real, there are no real solutions for $y_1$ in this case.
Thus, if $b^2 < 4a^2$, there is only one midpoint $(0,0)$, corresponding to only one chord. This contradicts the condition of exactly three chords.

If $b^2 > 4a^2$, then $b^2 - 4a^2 > 0$.
$y_1^2 = \frac{4a^2}{b^2} (b^2 - 4a^2)$ gives two distinct real values for $y_1$:
$y_1 = \pm \frac{2a}{b} \sqrt{b^2 - 4a^2}$.
The corresponding $x_1$ value is $x_{1, \text{new}} = a - \frac{4a^3}{b^2}$.
Since $b^2 > 4a^2$, we have $\frac{4a^2}{b^2} < 1$.
$x_{1, \text{new}} = a(1 - \frac{4a^2}{b^2})$. Since $a>0$ and $1 - \frac{4a^2}{b^2} > 0$, $x_{1, \text{new}} > 0$.
Also, since $b^2 > 4a^2$, $b^2 - 4a^2 > 0$, so $y_1 = \pm \frac{2a}{b} \sqrt{b^2 - 4a^2}$ are non-zero.
So, we have two distinct midpoints: $(x_{1, \text{new}}, y_{1, \text{new}})$ and $(x_{1, \text{new}}, -y_{1, \text{new}})$, where $y_{1, \text{new}} = \frac{2a}{b} \sqrt{b^2 - 4a^2} \ne 0$.
These two midpoints are distinct from $(0,0)$ because $x_{1, \text{new}} > 0$.
Thus, when $b^2 > 4a^2$, we have three distinct midpoints: $(0,0)$, $(a - \frac{4a^3}{b^2}, \frac{2a}{b} \sqrt{b^2 - 4a^2})$, and $(a - \frac{4a^3}{b^2}, -\frac{2a}{b} \sqrt{b^2 - 4a^2})$.
Each distinct midpoint corresponds to a unique chord.
We also checked in the thought process that any point $(x_1, y_1)$ satisfying $b^2 x_1^2 - ab^2 x_1 + a^2 y_1^2 = 0$ is a valid midpoint of a chord passing through $(a,0)$ (the point $(x_1, y_1)$ lies inside or on the ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$).

Therefore, for there to be exactly three chords passing through $(a,0)$ bisected by the parabola $y^2=4ax$, we must have $b^2 > 4a^2$.