Question

Let $I_1 = \int_0^{\frac{\pi}{4}} e^{x^2} dx, I_2 = \int_0^{\frac{\pi}{4}} e^x dx, I_3 = \int_0^{\frac{\pi}{4}} e^{x^2} \cdot \cos x dx, I_4 = \int_0^{\frac{\pi}{4}} e^{x^2} \cdot \sin x dx$, then:

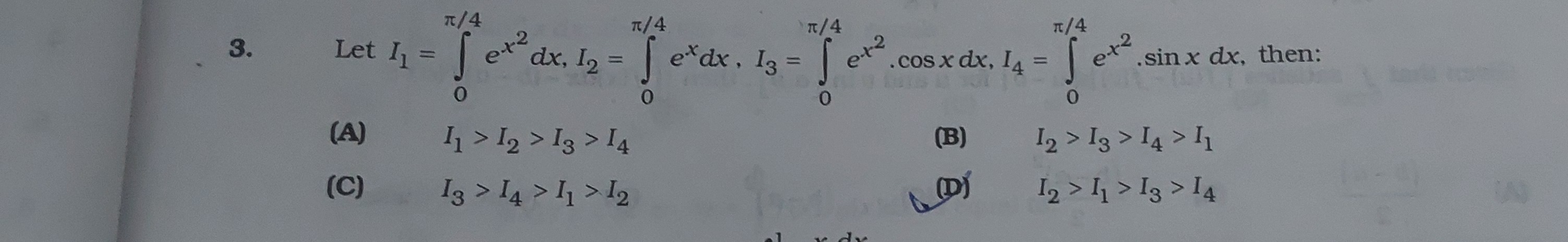
• A. $I_1 > I_2 > I_3 > I_4$
• B. $I_2 > I_3 > I_4 > I_1$
• C. $I_3 > I_4 > I_1 > I_2$
• D. $I_2 > I_1 > I_3 > I_4$

Answer 1

Answer: (D)

I_2 > I_1 > I_3 > I_4

Answer 2

To compare the four given definite integrals, we will analyze their integrands over the interval of integration $[0, \frac{\pi}{4}]$.

The integrals are:

1. $I_1 = \int_0^{\frac{\pi}{4}} e^{x^2} dx$
2. $I_2 = \int_0^{\frac{\pi}{4}} e^x dx$
3. $I_3 = \int_0^{\frac{\pi}{4}} e^{x^2} \cdot \cos x dx$
4. $I_4 = \int_0^{\frac{\pi}{4}} e^{x^2} \cdot \sin x dx$

The interval of integration is $[0, \frac{\pi}{4}]$. Note that $\frac{\pi}{4} \approx 0.785$, which is less than 1.

Step 1: Comparing $I_1$ and $I_2$

For $x \in (0, \frac{\pi}{4}]$, we have $x^2 < x$ (since $x < 1$).

Since the exponential function $e^t$ is strictly increasing, if $a < b$, then $e^a < e^b$.

Therefore, for $x \in (0, \frac{\pi}{4}]$, $e^{x^2} < e^x$.

By the property of definite integrals, if $f(x) < g(x)$ over an interval, then $\int f(x) dx < \int g(x) dx$.

So, $\int_0^{\frac{\pi}{4}} e^{x^2} dx < \int_0^{\frac{\pi}{4}} e^x dx$, which means $I_1 < I_2$.

Step 2: Comparing $I_1$ and $I_3$

For $x \in (0, \frac{\pi}{4}]$, we know that $\cos x < 1$. (At $x=0$, $\cos 0 = 1$, but for any $x > 0$ in the interval, $\cos x < 1$).

Since $e^{x^2}$ is always positive, multiplying both sides of $\cos x < 1$ by $e^{x^2}$ gives:

$e^{x^2} \cdot \cos x < e^{x^2}$.

Therefore, $\int_0^{\frac{\pi}{4}} e^{x^2} \cdot \cos x dx < \int_0^{\frac{\pi}{4}} e^{x^2} dx$, which means $I_3 < I_1$.

Step 3: Comparing $I_3$ and $I_4$

For $x \in (0, \frac{\pi}{4})$, we know that $\cos x > \sin x$. (At $x=0$, $\cos 0 = 1$ and $\sin 0 = 0$. At $x=\frac{\pi}{4}$, $\cos \frac{\pi}{4} = \sin \frac{\pi}{4} = \frac{1}{\sqrt{2}}$. The strict inequality $\cos x > \sin x$ holds for $x \in (0, \frac{\pi}{4})$).

Since $e^{x^2}$ is always positive, multiplying both sides of $\cos x > \sin x$ by $e^{x^2}$ gives:

$e^{x^2} \cdot \cos x > e^{x^2} \cdot \sin x$.

Therefore, $\int_0^{\frac{\pi}{4}} e^{x^2} \cdot \cos x dx > \int_0^{\frac{\pi}{4}} e^{x^2} \cdot \sin x dx$, which means $I_3 > I_4$.

Step 4: Combining the inequalities

From Step 1, we have $I_2 > I_1$.

From Step 2, we have $I_1 > I_3$.

From Step 3, we have $I_3 > I_4$.

Combining these inequalities, we get the final order:

$I_2 > I_1 > I_3 > I_4$.

Comparing this with the given options, option (D) matches our result.