Question
Question: Let f be a differentiable function on R and satisfying the integral equation $\int_{0}^{x}f(t)dt + \...
Let f be a differentiable function on R and satisfying the integral equation ∫0xf(t)dt+∫0xt⋅f(x−t)dt=−1+e−x, for all x∈R, then
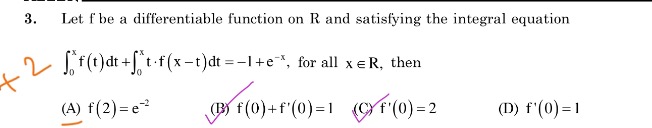
f(2) = e−2
f(0)+f'(0) = 1
f'(0) = 2
f'(0) = 1
Options (A), (B), and (C) are correct.
Solution
-
Rewrite the given equation:
∫0xf(t)dt+∫0xtf(x−t)dt=−1+e−x.Change variable in the second integral using u=x−t so that
∫0xtf(x−t)dt=∫0x(x−u)f(u)du.Hence, the equation becomes:
∫0x[1+(x−u)]f(u)du=∫0x[(x+1)−u]f(u)du=e−x−1. -
Differentiate both sides with respect to x. Use Leibniz’s rule:
dxd[∫0x[(x+1)−u]f(u)du]=∫0xf(u)du+f(x)(since (x+1)−x=1).And the derivative of the right side is:
dxd[e−x−1]=−e−x.So, we have:
∫0xf(u)du+f(x)=−e−x. -
Let F(x)=∫0xf(u)du, then F′(x)=f(x). The equation becomes:
F(x)+F′(x)=−e−x.This is a first-order linear ODE for F(x).
-
Solve using the integrating factor ex:
dxd[exF(x)]=−exe−x=−1.Integrate:
exF(x)=−x+C.Since F(0)=0, we have C=0. Thus:
F(x)=−xe−x. -
Differentiate F(x) to find f(x):
f(x)=F′(x)=dxd[−xe−x]=−e−x+xe−x=e−x(x−1). -
Now check the options:
-
f(2)=e−2(2−1)=e−2. So option (A) is correct.
-
f(0)=e0(0−1)=−1 and f′(x)=dxd[e−x(x−1)]=e−x(2−x) giving f′(0)=2. Thus, f(0)+f′(0)=−1+2=1. So option (B) is correct.
-
f′(0)=2 confirms option (C) is correct.
-
Option (D) f′(0)=1 is false.
-
