Question
Question: $\int \sqrt{z}\left(z^{2}-\frac{1}{4z}\right)dz =$...
∫z(z2−4z1)dz=
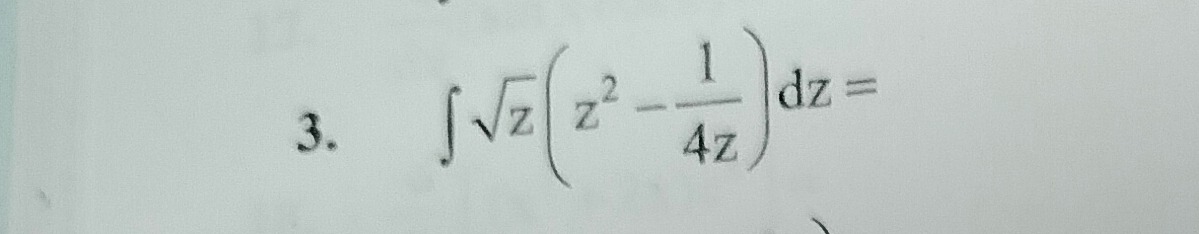
72z7/2−21z1/2+C
Solution
We need to evaluate the integral ∫z(z2−4z1)dz.
First, simplify the integrand: z(z2−4z1)=z1/2(z2−41z−1) =z1/2⋅z2−z1/2⋅41z−1
Using the exponent rule am⋅an=am+n: =z1/2+2−41z1/2−1 =z5/2−41z−1/2
Now, integrate the simplified expression term by term using the power rule for integration, ∫zndz=n+1zn+1+C (for n=−1): ∫(z5/2−41z−1/2)dz=∫z5/2dz−41∫z−1/2dz
For the first term, n=5/2: ∫z5/2dz=5/2+1z5/2+1+C1=7/2z7/2+C1=72z7/2+C1
For the second term, n=−1/2: ∫z−1/2dz=−1/2+1z−1/2+1+C2=1/2z1/2+C2=2z1/2+C2
Combine the results: ∫(z5/2−41z−1/2)dz=72z7/2−41(2z1/2)+C =72z7/2−21z1/2+C where C is the constant of integration.
In summary: Simplify the integrand using exponent rules. Apply the power rule for integration ∫zndz=n+1zn+1 to each term.
