Question

$\int \sqrt{z} \left( z^2 - \frac{1}{4z} \right) dz =$

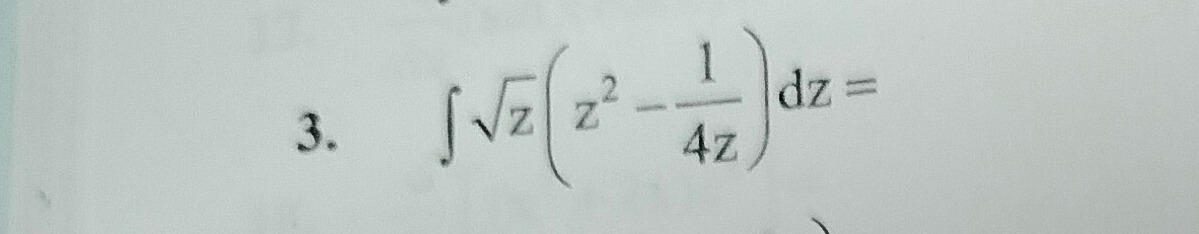
Answer 1

$\frac{2}{7} z^{7/2} - \frac{1}{2} z^{1/2} + C$

Answer 2

The integrand is simplified by distributing $\sqrt{z} = z^{1/2}$ into the parenthesis and using the exponent rule $a^m a^n = a^{m+n}$. This transforms the integrand into a sum of power functions: $z^{5/2} - \frac{1}{4} z^{-1/2}$. The integral is then evaluated term by term using the power rule for integration $\int z^n dz = \frac{z^{n+1}}{n+1} + C$.