Question

$\int sin(logx)dx$ is equal to:

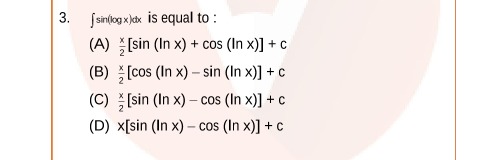
• A. $\frac{x}{2}$[sin (In x) + cos (In x)] + c
• B. $\frac{x}{2}$[cos (In x) - sin (In x)] + c
• C. $\frac{x}{2}$[sin (In x) - cos (In x)] + c
• D. x[sin (In x) - cos (In x)] + c

Answer 1

Answer: (C)

$\frac{x}{2}$[sin (In x) - cos (In x)] + c

Answer 2

Let $I = \int \sin(\log x) dx$. Using integration by parts twice, we find $2I = x\sin(\log x) - x\cos(\log x)$, which gives $I = \frac{x}{2}[\sin(\log x) - \cos(\log x)] + c$.