Question

If $Z_1, Z_2, Z_3, Z_4$ are roots of the equation $z^4 + z^3 + z^2 + z + 1 = 0$, then least value of $[|Z_1 + Z_2|] + 1$ is ([.] denotes G.I.F.) ___ .

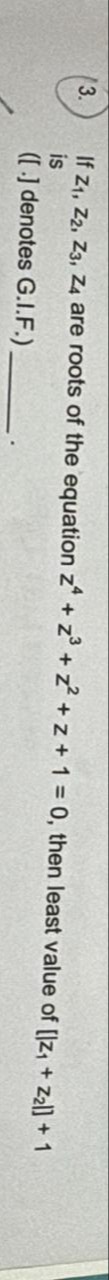
Answer 1

1

Answer 2

The equation

$$z^4+z^3+z^2+z+1=0$$

can be written as

$$\frac{z^5-1}{z-1}=0,$$

so its roots are the 5th roots of unity, except $z=1$. That is,

$$z_k = e^{2\pi i k/5},\quad k=1,2,3,4.$$

For any two roots, say $z_a$ and $z_b$, we have:

$$|z_a+z_b| = \left|e^{i\theta_a}+e^{i\theta_b}\right| = 2\left|\cos\frac{\theta_a-\theta_b}{2}\right|.$$

Choosing two roots with an angular difference of $144^\circ$ (or $216^\circ$) gives:

$$|z_a+z_b| = 2\left|\cos(72^\circ)\right| \approx 2(0.309) \approx 0.618.$$

Since the Greatest Integer Function (G.I.F) $[x]$ gives the greatest integer $\le x$,

$$[|z_a+z_b|] = [0.618] = 0.$$

Thus, the least value of $[|z_1+z_2|]+1$ is

$$0+1=1.$$