Question

If the differential equation of a curve, passing through $(0, -\pi/4)$ and $(t, 0)$ is

$\cos y \left( \frac{dy}{dx} + e^{-x} \right) + \sin y \left( e^{-x} - \frac{dy}{dx} \right) = e^{-x}$,

then find the value of $t.e^{-t}$.

Answer 1

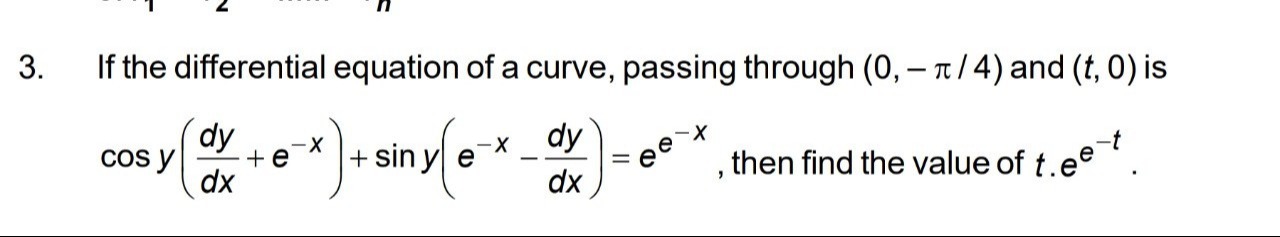
-(1+ln 2)ln(1+ln 2)

Answer 2

The given differential equation is:

$\cos y \left( \frac{dy}{dx} + e^{-x} \right) + \sin y \left( e^{-x} - \frac{dy}{dx} \right) = e^{-x}$

Expand the terms:

$\cos y \frac{dy}{dx} + e^{-x} \cos y + e^{-x} \sin y - \sin y \frac{dy}{dx} = e^{-x}$

Group the terms with $\frac{dy}{dx}$ and $e^{-x}$:

$(\cos y - \sin y) \frac{dy}{dx} + e^{-x} (\cos y + \sin y) = e^{-x}$

Let $u = \sin y + \cos y$. Then, differentiate $u$ with respect to $x$:

$\frac{du}{dx} = \frac{d}{dx}(\sin y + \cos y) = \cos y \frac{dy}{dx} - \sin y \frac{dy}{dx} = (\cos y - \sin y) \frac{dy}{dx}$

Substitute $u$ and $\frac{du}{dx}$ into the differential equation:

$\frac{du}{dx} + e^{-x} u = e^{-x}$

The integrating factor (IF) is given by:

$\text{IF} = e^{\int P(x) dx} = e^{\int e^{-x} dx} = e^{-e^{-x}}$

The general solution is given by $u \cdot \text{IF} = \int Q(x) \cdot \text{IF} dx + C$:

$u e^{-e^{-x}} = \int e^{-x} e^{-e^{-x}} dx + C$

To evaluate the integral $\int e^{-x} e^{-e^{-x}} dx$, let $v = e^{-x}$. Then $dv = -e^{-x} dx$, so $e^{-x} dx = -dv$. The integral becomes:

$\int e^{-v} (-dv) = -\int e^{-v} dv = -(-e^{-v}) = e^{-v}$

Substitute back $v = e^{-x}$:

$\int e^{-x} e^{-e^{-x}} dx = e^{-e^{-x}}$

So, the general solution is:

$u e^{-e^{-x}} = e^{-e^{-x}} + C$

Divide by $e^{-e^{-x}}$:

$u = 1 + C e^{e^{-x}}$

Substitute back $u = \sin y + \cos y$:

$\sin y + \cos y = 1 + C e^{e^{-x}}$

Now, use the given points to find the constant $C$. The curve passes through $(0, -\pi/4)$. Substitute $x=0$ and $y=-\pi/4$:

$\sin(-\pi/4) + \cos(-\pi/4) = 1 + C e^{e^{-0}}$

$-\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} = 1 + C e^{1}$

$0 = 1 + Ce$

$Ce = -1 \implies C = -\frac{1}{e}$

So, the particular solution is:

$\sin y + \cos y = 1 - \frac{1}{e} e^{e^{-x}}$

$\sin y + \cos y = 1 - e^{e^{-x}-1}$

The curve also passes through $(t, 0)$. Substitute $x=t$ and $y=0$:

$\sin(0) + \cos(0) = 1 - e^{e^{-t}-1}$

$0 + 1 = 1 - e^{e^{-t}-1}$

$1 = 1 - e^{e^{-t}-1}$

$e^{e^{-t}-1} = 0$

This result is mathematically impossible. An exponential function can never be equal to zero. There is likely a typo in the question.

Assuming the solution is $\sin y + \cos y = -1 + C e^{e^{-x}}$.

Using the point $(0, -\pi/4)$:

$\sin(-\pi/4) + \cos(-\pi/4) = -1 + C e^{e^0}$

$-\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} = -1 + C e^1$

$0 = -1 + Ce \implies Ce = 1 \implies C = \frac{1}{e}$.

So the particular solution is:

$\sin y + \cos y = -1 + \frac{1}{e} e^{e^{-x}} = -1 + e^{e^{-x}-1}$.

Using the point $(t, 0)$:

$\sin(0) + \cos(0) = -1 + e^{e^{-t}-1}$

$0 + 1 = -1 + e^{e^{-t}-1}$

$1 = -1 + e^{e^{-t}-1}$

$2 = e^{e^{-t}-1}$

Take natural logarithm on both sides:

$\ln 2 = e^{-t} - 1$

$e^{-t} = 1 + \ln 2$

We need to find the value of $t \cdot e^{-t}$.

From $e^{-t} = 1 + \ln 2$, we find $t$:

$-t = \ln(1 + \ln 2)$

$t = -\ln(1 + \ln 2)$

Now, calculate $t \cdot e^{-t}$:

$t \cdot e^{-t} = (-\ln(1 + \ln 2)) \cdot (1 + \ln 2)$

This is the most plausible interpretation that yields a numerical answer.