Question
Question: If $px^4+qx^3+rx^2+sx+t = \begin{vmatrix} x^2+3x & x-1 & x+3 \\ x+1 & 2-x & x-3 \\ x-3 & x+4 & 3x \e...
If px4+qx3+rx2+sx+t=x2+3xx+1x−3x−12−xx+4x+3x−33x then t is equal to -
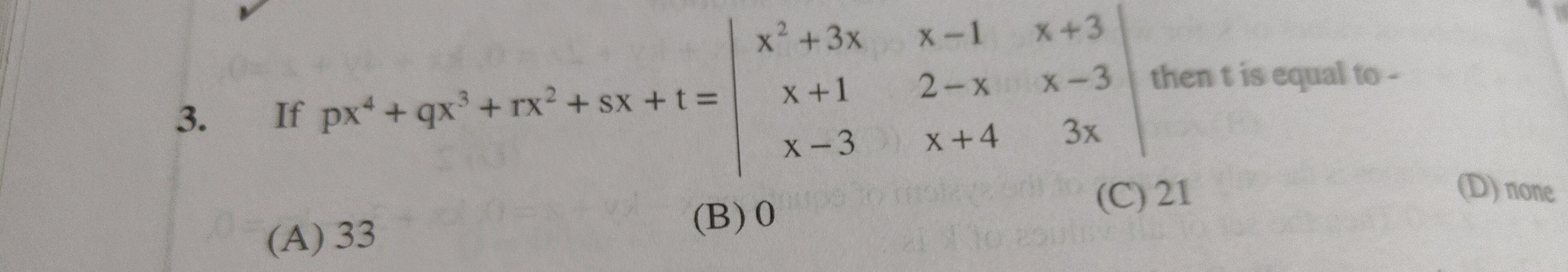
33
0
21
none
21
Solution
To find the value of 't', we need to understand that 't' is the constant term of the polynomial px4+qx3+rx2+sx+t.
The constant term of any polynomial P(x) can be found by substituting x=0 into the polynomial.
Let the given polynomial be P(x)=px4+qx3+rx2+sx+t.
Then, P(0)=p(0)4+q(0)3+r(0)2+s(0)+t=t.
We are given that P(x)=x2+3xx+1x−3x−12−xx+4x+3x−33x.
To find 't', we substitute x=0 into the determinant:
t=02+3(0)0+10−30−12−00+40+30−33(0)=01−3−1243−30
Now, we evaluate this 3×3 determinant. We can expand it along the first row:
t=0⋅cofactor(0)−(−1)⋅cofactor(−1)+3⋅cofactor(3)
t=0⋅24−30−(−1)⋅1−3−30+3⋅1−324
Calculate the 2×2 determinants:
24−30=(2)(0)−(−3)(4)=0−(−12)=12
1−3−30=(1)(0)−(−3)(−3)=0−9=−9
1−324=(1)(4)−(2)(−3)=4−(−6)=4+6=10
Substitute these values back into the expression for 't':
t=0⋅(12)+1⋅(−9)+3⋅(10)
t=0−9+30
t=21
