Question

3. If cos⁻¹x + cos⁻¹y + cos⁻¹z = x, then

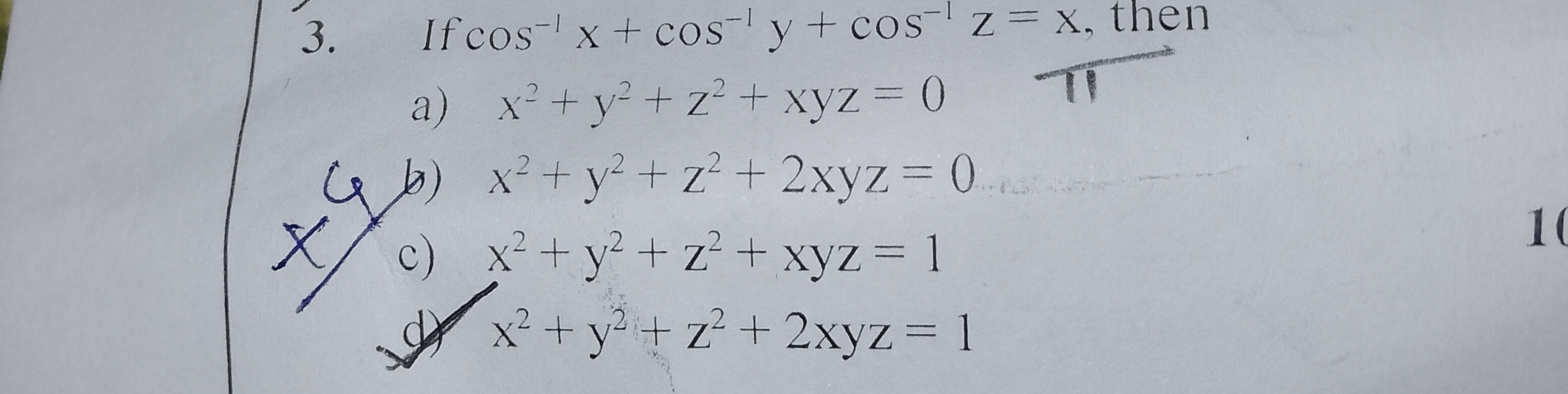
• A. x² + y² + z² + xyz = 0
• B. x² + y² + z² + 2xyz = 0
• C. x² + y² + z² + xyz = 1
• D. x² + y² + z² + 2xyz = 1

Answer 1

Answer: (D)

x² + y² + z² + 2xyz = 1

Answer 2

Explanation:
Using the standard identity for inverse cosine functions, when

$$\cos^{-1}x+\cos^{-1}y+\cos^{-1}z=\pi,$$

one obtains

$$x^2+y^2+z^2+2xyz=1.$$

In the given problem the sum is equated to $x$, but following the same approach as the similar question (where the sum equals $\pi$), we conclude that the correct option is the one that gives

$$x^2+y^2+z^2+2xyz=1.$$

Answer: Option d) $x^2+y^2+z^2+2xyz=1$.