Question
Question: If $a = \cos \theta + i \sin \theta, b = \cos 2\theta - i \sin 2\theta$ and $c = \cos 3\theta + i \s...
If a=cosθ+isinθ,b=cos2θ−isin2θ and c=cos3θ+isin3θ such that if abcbcacab=0, then
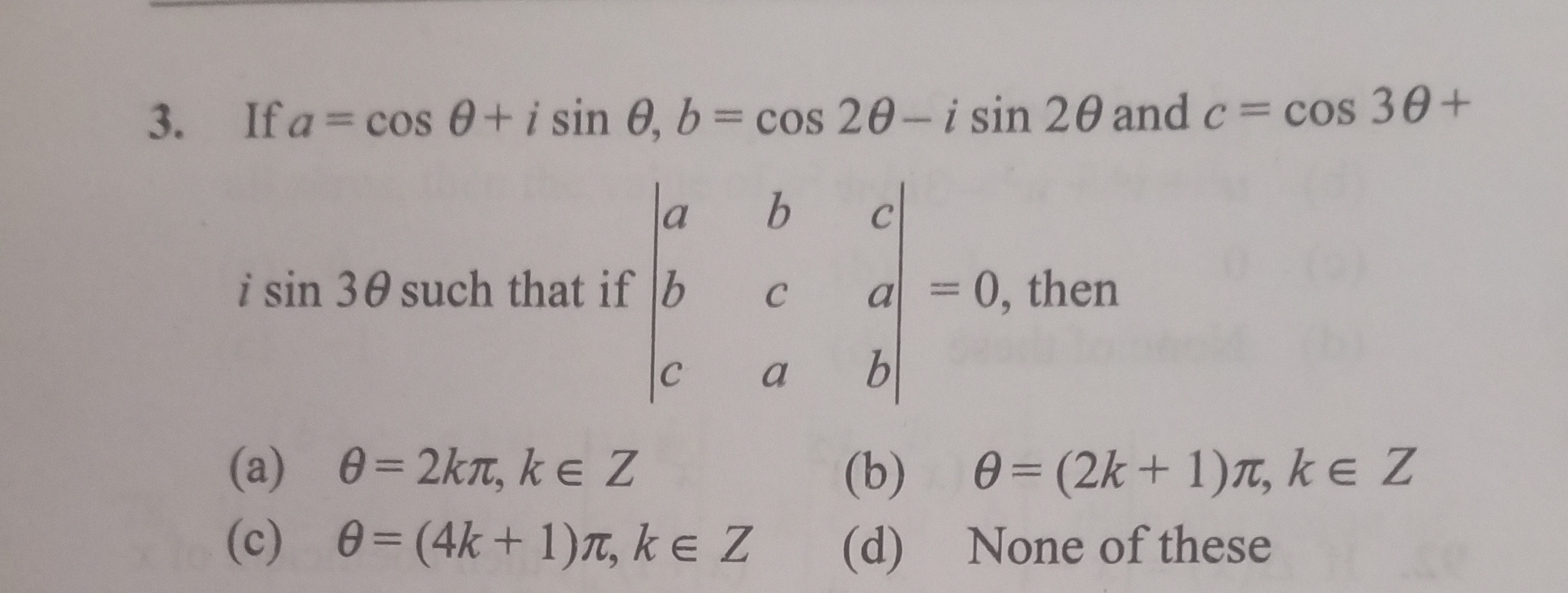
θ=2kπ,k∈Z
θ=(2k+1)π,k∈Z
θ=(4k+1)π,k∈Z
None of these
(a) θ=2kπ,k∈Z
Solution
The given complex numbers are: a=cosθ+isinθ=eiθ b=cos2θ−isin2θ=cos(−2θ)+isin(−2θ)=e−i2θ c=cos3θ+isin3θ=ei3θ
The determinant given is: D=abcbcacab
This is a cyclic determinant. The value of this determinant is given by the formula: D=3abc−(a3+b3+c3)
We are given that D=0. So, 3abc−(a3+b3+c3)=0 This can be rewritten as a3+b3+c3−3abc=0.
We know the algebraic identity: a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ca)
So, the condition D=0 implies: (a+b+c)(a2+b2+c2−ab−bc−ca)=0
This means either a+b+c=0 or a2+b2+c2−ab−bc−ca=0.
The second condition, a2+b2+c2−ab−bc−ca=0, can be rewritten as: 21[(a−b)2+(b−c)2+(c−a)2]=0 For this sum of squares to be zero, each term must be zero (since a,b,c are complex numbers, this holds if they are real, or if we consider magnitude squared, but here it implies a−b=0, etc.). This implies a−b=0, b−c=0, and c−a=0, which means a=b=c.
Let's analyze the two possibilities:
Case 1: a=b=c If a=b, then eiθ=e−i2θ. This implies eiθ/e−i2θ=1, so ei(θ−(−2θ))=1. ei3θ=1. This means 3θ=2kπ for some integer k∈Z. So, θ=32kπ.
If b=c, then e−i2θ=ei3θ. This implies ei3θ/e−i2θ=1, so ei(3θ−(−2θ))=1. ei5θ=1. This means 5θ=2mπ for some integer m∈Z. So, θ=52mπ.
For a=b=c to hold, both conditions for θ must be satisfied: 32kπ=52mπ 3k=5m 5k=3m. Since 3 and 5 are coprime, k must be a multiple of 3. Let k=3n for some integer n∈Z. Substituting k=3n into θ=32kπ: θ=32(3n)π=2nπ.
Let's check if θ=2nπ satisfies a=b=c: a=ei(2nπ)=cos(2nπ)+isin(2nπ)=1+i(0)=1. b=e−i2(2nπ)=e−i4nπ=cos(−4nπ)+isin(−4nπ)=1+i(0)=1. c=ei3(2nπ)=ei6nπ=cos(6nπ)+isin(6nπ)=1+i(0)=1. Indeed, a=b=c=1 when θ=2nπ. This is a valid set of solutions. This matches option (a).
Case 2: a+b+c=0 eiθ+e−i2θ+ei3θ=0 This implies (cosθ+isinθ)+(cos2θ−isin2θ)+(cos3θ+isin3θ)=0. Separating real and imaginary parts: (cosθ+cos2θ+cos3θ)+i(sinθ−sin2θ+sin3θ)=0. For this to be true, both real and imaginary parts must be zero.
Real part: cosθ+cos2θ+cos3θ=0 (cosθ+cos3θ)+cos2θ=0 Using cosA+cosB=2cos(2A+B)cos(2A−B): 2cos(2θ+3θ)cos(23θ−θ)+cos2θ=0 2cos2θcosθ+cos2θ=0 cos2θ(2cosθ+1)=0. This implies either cos2θ=0 or 2cosθ+1=0.
Imaginary part: sinθ−sin2θ+sin3θ=0 (sinθ+sin3θ)−sin2θ=0 Using sinA+sinB=2sin(2A+B)cos(2A−B): 2sin(2θ+3θ)cos(23θ−θ)−sin2θ=0 2sin2θcosθ−sin2θ=0 sin2θ(2cosθ−1)=0. This implies either sin2θ=0 or 2cosθ−1=0.
Now we need to find θ that satisfies both conditions simultaneously:
- (cos2θ=0 or 2cosθ+1=0)
- (sin2θ=0 or 2cosθ−1=0)
Let's check the combinations: Subcase 2.1: cos2θ=0 If cos2θ=0, then 2θ=(n+21)π, which implies sin2θ=±1=0. For the second equation sin2θ(2cosθ−1)=0 to hold, we must have 2cosθ−1=0, so cosθ=1/2. If cosθ=1/2, then θ=2kπ±3π. Then 2θ=4kπ±32π. cos2θ=cos(±32π)=−1/2. This contradicts cos2θ=0. So, this subcase yields no solution.
Subcase 2.2: 2cosθ+1=0 If 2cosθ+1=0, then cosθ=−1/2. Then 2cosθ−1=2(−1/2)−1=−1−1=−2=0. For the second equation sin2θ(2cosθ−1)=0 to hold, we must have sin2θ=0. If sin2θ=0, then 2θ=nπ, so θ=nπ/2. If θ=nπ/2, then cosθ can be 0,1,−1. However, we need cosθ=−1/2. This is not possible for θ=nπ/2. So, this subcase also yields no solution.
Since both subcases for a+b+c=0 lead to contradictions, there are no solutions for θ when a+b+c=0.
Therefore, the only valid solutions come from a=b=c, which gives θ=2kπ, where k∈Z.
The final answer is (a).
