Question

If a, b, c are positive numbers such that $a^{\log_3 7} = 27$, $b^{\log_7 11} = 49$, $c^{\log_{11} 25} = \sqrt{11}$, then the sum of digits of $S = a^{(\log_3 7)^2} + b^{(\log_7 11)^2} + c^{(\log_{11} 25)^2}$ is:

Answer 1

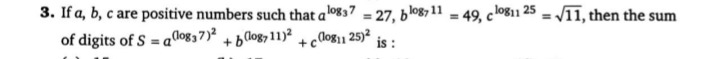
19

Answer 2

The problem requires us to evaluate an expression $S$ and then find the sum of its digits. We are given three equations involving exponents and logarithms.

Let's break down the calculation for each term in $S = a^{(\log_3 7)^2} + b^{(\log_7 11)^2} + c^{(\log_{11} 25)^2}$.

First Term: $a^{(\log_3 7)^2}$

Given: $a^{\log_3 7} = 27$. Let $x = \log_3 7$. Then the given equation is $a^x = 27$. The first term can be written as $a^{x^2} = (a^x)^x$. Substitute $a^x = 27$: First Term $= 27^x = 27^{\log_3 7}$. We know that $27 = 3^3$. So, First Term $= (3^3)^{\log_3 7}$ Apply the exponent rule $(p^m)^n = p^{mn}$: First Term $= 3^{3 \log_3 7}$ Apply the logarithm rule $k \log_b M = \log_b (M^k)$: First Term $= 3^{\log_3 (7^3)}$ Apply the logarithm property $b^{\log_b M} = M$: First Term $= 7^3 = 343$.

Second Term: $b^{(\log_7 11)^2}$

Given: $b^{\log_7 11} = 49$. Let $y = \log_7 11$. Then the given equation is $b^y = 49$. The second term can be written as $b^{y^2} = (b^y)^y$. Substitute $b^y = 49$: Second Term $= 49^y = 49^{\log_7 11}$. We know that $49 = 7^2$. So, Second Term $= (7^2)^{\log_7 11}$ Apply the exponent rule $(p^m)^n = p^{mn}$: Second Term $= 7^{2 \log_7 11}$ Apply the logarithm rule $k \log_b M = \log_b (M^k)$: Second Term $= 7^{\log_7 (11^2)}$ Apply the logarithm property $b^{\log_b M} = M$: Second Term $= 11^2 = 121$.

Third Term: $c^{(\log_{11} 25)^2}$

Given: $c^{\log_{11} 25} = \sqrt{11}$. Let $z = \log_{11} 25$. Then the given equation is $c^z = \sqrt{11}$. The third term can be written as $c^{z^2} = (c^z)^z$. Substitute $c^z = \sqrt{11}$: Third Term $= (\sqrt{11})^z = (\sqrt{11})^{\log_{11} 25}$. We know that $\sqrt{11} = 11^{1/2}$. So, Third Term $= (11^{1/2})^{\log_{11} 25}$ Apply the exponent rule $(p^m)^n = p^{mn}$: Third Term $= 11^{\frac{1}{2} \log_{11} 25}$ Apply the logarithm rule $k \log_b M = \log_b (M^k)$: Third Term $= 11^{\log_{11} (25^{1/2})}$ Since $25^{1/2} = \sqrt{25} = 5$: Third Term $= 11^{\log_{11} 5}$ Apply the logarithm property $b^{\log_b M} = M$: Third Term $= 5$.

Calculate S:

Now, sum the values of the three terms: $S = 343 + 121 + 5$ $S = 464 + 5$ $S = 469$.

Sum of digits of S:

The digits of $S = 469$ are 4, 6, and 9. Sum of digits $= 4 + 6 + 9 = 19$.