Solveeit Logo
Login

Question

Question: $\frac{{}^nC_0}{2}-\frac{{}^nC_1}{6}+\frac{{}^nC_2}{10}-\frac{{}^nC_3}{14}+.....+\frac{(-1)^n {}^nC_...

nC02−nC16+nC210−nC314+.....+(−1)nnCn(4n+2)\frac{{}^nC_0}{2}-\frac{{}^nC_1}{6}+\frac{{}^nC_2}{10}-\frac{{}^nC_3}{14}+.....+\frac{(-1)^n {}^nC_n}{(4n+2)}, n∈Nn \in N is equal to :

A

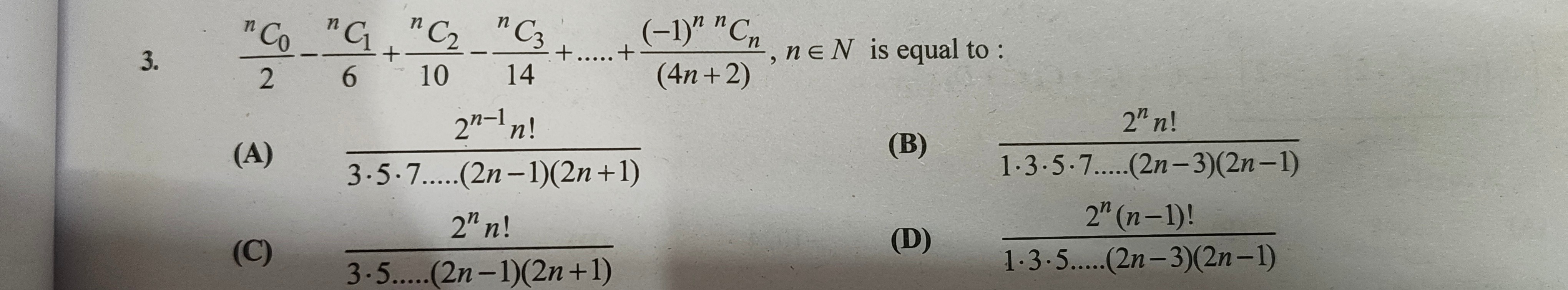
2n−1n!3⋅5⋅7.....(2n−1)(2n+1)\frac{2^{n-1} n!}{3 \cdot 5 \cdot 7.....(2n-1)(2n+1)}

B

2nn!1⋅3⋅5⋅7.....(2n−3)(2n−1)\frac{2^n n!}{1 \cdot 3 \cdot 5 \cdot 7.....(2n-3)(2n-1)}

C

2nn!3⋅5.....(2n−1)(2n+1)\frac{2^n n!}{3 \cdot 5.....(2n-1)(2n+1)}

D

2n(n−1)!1⋅3⋅5.....(2n−3)(2n−1)\frac{2^n (n-1)!}{1 \cdot 3 \cdot 5.....(2n-3)(2n-1)}

Answer

2n−1n!3⋅5⋅7.....(2n−1)(2n+1)\frac{2^{n-1} n!}{3 \cdot 5 \cdot 7.....(2n-1)(2n+1)}

Explanation

Solution

We wish to evaluate

S=nC02−nC16+nC210−nC314+⋯+(−1)n nCn4n+2.S=\frac{{}^nC_0}{2}-\frac{{}^nC_1}{6}+\frac{{}^nC_2}{10}-\frac{{}^nC_3}{14}+\cdots+\frac{(-1)^n\,{}^nC_n}{4n+2}.

Notice that

4k+2=2(2k+1).4k+2=2(2k+1).

Thus we can write

S=12∑k=0n(−1)k(nk)2k+1.S=\frac{1}{2}\sum_{k=0}^n\frac{(-1)^k\binom{n}{k}}{2k+1}.

Recall that

12k+1=∫01x2k dx.\frac{1}{2k+1}=\int_0^1 x^{2k}\,dx.

Then,

S=12∑k=0n(−1)k(nk)∫01x2k dx=12∫01∑k=0n(−1)k(nk)x2k dx.S=\frac{1}{2}\sum_{k=0}^n (-1)^k\binom{n}{k}\int_0^1 x^{2k}\,dx =\frac{1}{2}\int_0^1\sum_{k=0}^n(-1)^k\binom{n}{k}x^{2k}\,dx.

But

∑k=0n(−1)k(nk)x2k=(1−x2)n.\sum_{k=0}^n(-1)^k\binom{n}{k}x^{2k} = (1-x^2)^n.

Hence,

S=12∫01(1−x2)n dx.S=\frac{1}{2}\int_0^1 (1-x^2)^n\,dx.

Letting u=x2u=x^2 so that du=2x dxdu = 2x\,dx or dx=du2udx = \frac{du}{2\sqrt{u}} and changing limits (x=0⇒u=0x=0 \Rightarrow u=0, x=1⇒u=1x=1 \Rightarrow u=1), we get:

∫01(1−x2)n dx=12∫01u−1/2(1−u)n du.\int_0^1(1-x^2)^n\,dx=\frac{1}{2}\int_0^1 u^{-1/2}(1-u)^n\,du.

This is the Beta integral:

12B(12,n+1)=12⋅Γ(1/2)Γ(n+1)Γ(n+32).\frac{1}{2} B\left(\frac{1}{2}, n+1\right) = \frac{1}{2}\cdot\frac{\Gamma(1/2)\Gamma(n+1)}{\Gamma\left(n+\frac{3}{2}\right)}.

Thus,

S=12⋅12⋅Γ(1/2)Γ(n+1)Γ(n+32)=Γ(1/2) n!4 Γ(n+32).S=\frac{1}{2}\cdot \frac{1}{2}\cdot\frac{\Gamma(1/2)\Gamma(n+1)}{\Gamma\left(n+\frac{3}{2}\right)} =\frac{\Gamma(1/2)\, n!}{4\, \Gamma\left(n+\frac{3}{2}\right)}.

Using the relation

Γ(n+32)=(2n+1)!!2n+1πandΓ(1/2)=π,\Gamma\left(n+\frac{3}{2}\right)=\frac{(2n+1)!!}{2^{n+1}}\sqrt{\pi} \quad\text{and}\quad \Gamma(1/2)=\sqrt{\pi},

we have:

S=π n!4((2n+1)!!2n+1π)=2n+1n!4 (2n+1)!!=2n−1n!(2n+1)!!.S=\frac{\sqrt{\pi}\, n!}{4\left(\frac{(2n+1)!!}{2^{n+1}}\sqrt{\pi}\right)} =\frac{2^{n+1}n!}{4\,(2n+1)!!} =\frac{2^{n-1}n!}{(2n+1)!!}.

Since

(2n+1)!!=1⋅3⋅5⋯(2n+1),(2n+1)!!=1\cdot 3 \cdot 5 \cdots (2n+1),

we can write the final answer as

2n−1n!3⋅5⋅7⋯(2n−1)(2n+1).\frac{2^{n-1}n!}{3\cdot5\cdot7\cdots(2n-1)(2n+1)}.