Question
Question: Find the point of intersection of tangents drawn at the points (i) the points (2,-4) and $(\frac{1}{...
Find the point of intersection of tangents drawn at the points (i) the points (2,-4) and (21,−2) of the parabola y2=8x (ii) the points (-2,2) and (-8,-4) of parabola y2=−2x.
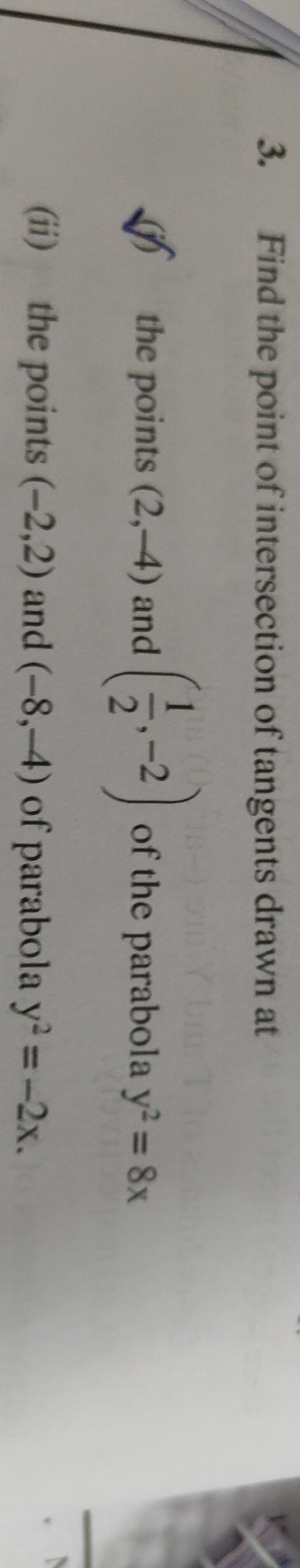
(i) (1, -3) and (ii) (4, -1)
(i) (1, 3) and (ii) (-4, 1)
(i) (-1, -3) and (ii) (-4, -1)
(i) (1, -3) and (ii) (-4, 1)
(i) (1, -3) and (ii) (4, -1)
Solution
Part (i): Parabola y2=8x
Comparing with y2=4ax, we get 4a=8, so a=2. The general equation of the tangent to the parabola y2=4ax at a point (x1,y1) is yy1=2a(x+x1).
-
Tangent at (2,−4): Using the tangent equation with x1=2,y1=−4,a=2: y(−4)=2(2)(x+2) −4y=4(x+2) −y=x+2⟹y=−x−2 (Equation 1)
-
Tangent at (21,−2): Using the tangent equation with x1=21,y1=−2,a=2: y(−2)=2(2)(x+21) −2y=4(x+21) −y=2(x+21) −y=2x+1⟹y=−2x−1 (Equation 2)
-
Point of Intersection: Equating Equation 1 and Equation 2: −x−2=−2x−1 2x−x=−1+2 x=1 Substitute x=1 into Equation 1: y=−(1)−2=−3 The point of intersection for part (i) is (1,−3).
Part (ii): Parabola y2=−2x
Comparing with y2=4ax, we get 4a=−2, so a=−21.
-
Tangent at (−2,2): Using the tangent equation with x1=−2,y1=2,a=−21: y(2)=2(−21)(x+(−2)) 2y=−1(x−2) 2y=−x+2⟹y=−21x+1 (Equation 3)
-
Tangent at (−8,−4): Using the tangent equation with x1=−8,y1=−4,a=−21: y(−4)=2(−21)(x+(−8)) −4y=−1(x−8) −4y=−x+8⟹y=41x−2 (Equation 4)
-
Point of Intersection: Equating Equation 3 and Equation 4: −21x+1=41x−2 Multiply by 4 to clear denominators: −2x+4=x−8 12=3x x=4 Substitute x=4 into Equation 3: y=−21(4)+1=−2+1=−1 The point of intersection for part (ii) is (4,−1).
Summary: (i) The point of intersection is (1,−3). (ii) The point of intersection is (4,−1).
