Question

Find the equations to the normals of ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ at the ends of the latera recta, and prove that each passes through an end of the minor axis if $e^4 + e^2 = 1$.

Answer 1

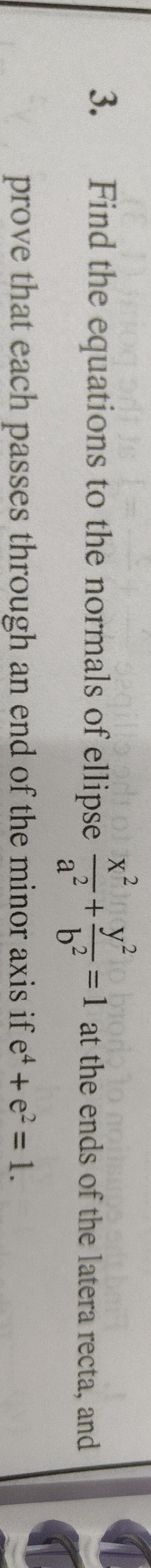
The equations of the normals are $x \pm ey = \pm ae^3$. If $e^4 + e^2 = 1$, which implies $e^2 = b/a$, then each normal passes through an end of the minor axis.

Answer 2

The ends of the latera recta are $(\pm ae, \pm \frac{b^2}{a})$. The equation of the normal to the ellipse at $(x_1, y_1)$ is $\frac{a^2 x}{x_1} - \frac{b^2 y}{y_1} = a^2 - b^2 = a^2 e^2$.

For the point $(ae, \frac{b^2}{a})$, the normal is $\frac{a^2 x}{ae} - \frac{b^2 y}{b^2/a} = a^2 e^2$, which simplifies to $x - ey = ae^3$.

For the point $(ae, -\frac{b^2}{a})$, the normal is $\frac{a^2 x}{ae} - \frac{b^2 y}{-b^2/a} = a^2 e^2$, which simplifies to $x + ey = ae^3$.

For the point $(-ae, \frac{b^2}{a})$, the normal is $\frac{a^2 x}{-ae} - \frac{b^2 y}{b^2/a} = a^2 e^2$, which simplifies to $x + ey = -ae^3$.

For the point $(-ae, -\frac{b^2}{a})$, the normal is $\frac{a^2 x}{-ae} - \frac{b^2 y}{-b^2/a} = a^2 e^2$, which simplifies to $x - ey = -ae^3$.

Thus, the equations of the normals are $x \pm ey = \pm ae^3$.

If $e^4 + e^2 = 1$, then $e^2(e^2+1) = 1$. Also, $b^2 = a^2(1-e^2)$, so $\frac{b^2}{a^2} = 1-e^2$. From $e^4+e^2=1$, we have $e^4 = 1-e^2 = \frac{b^2}{a^2}$. Taking the square root gives $e^2 = \frac{b}{a}$.

The ends of the minor axis are $(0, \pm b)$. Check if $x - ey = ae^3$ passes through $(0, -b)$: $0 - e(-b) = eb$. We need $eb = ae^3$, which means $\frac{b}{a} = e^2$. This is true if $e^4+e^2=1$. Check if $x + ey = ae^3$ passes through $(0, b)$: $0 + eb = eb$. We need $eb = ae^3$, which means $\frac{b}{a} = e^2$. This is true if $e^4+e^2=1$. Similarly, the other two normals pass through the remaining ends of the minor axis.