Question

Find the domain of definition the following functions.

(i) $f(x) = \arccos \frac{2x}{1+x}$ (ii) $f(x) = \sqrt{\cos(\sin x)} + \sin^{-1} \frac{1+x^2}{2x}$

Answer 1

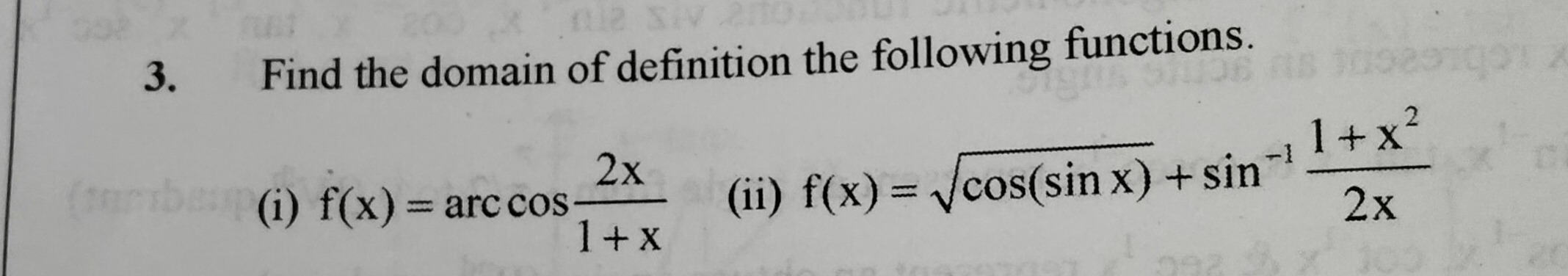
(i) [-1/3, 1], (ii) {-1, 1}

Answer 2

The domain of a function is the set of all possible input values (x) for which the function is defined. We need to consider the constraints imposed by the operations involved in the function definition.

(i) $f(x) = \arccos \frac{2x}{1+x}$

The function $\arccos(y)$ is defined for $y \in [-1, 1]$. Therefore, we must have the argument of the arccos function within this interval:

$-1 \le \frac{2x}{1+x} \le 1$

Also, the denominator cannot be zero, so $1+x \ne 0$, which means $x \ne -1$.

We split the inequality into two parts:

1. $\frac{2x}{1+x} \ge -1$

$\frac{2x}{1+x} + 1 \ge 0$

$\frac{2x + (1+x)}{1+x} \ge 0$

$\frac{3x + 1}{1+x} \ge 0$

This inequality holds when the numerator and denominator have the same sign, or when the numerator is zero.

The critical points are where the numerator or denominator is zero: $3x+1=0 \implies x = -1/3$, and $1+x=0 \implies x = -1$.

We analyze the sign of the expression $\frac{3x+1}{1+x}$ in the intervals determined by these points: $(-\infty, -1)$, $(-1, -1/3]$, $[-1/3, \infty)$.

• For $x < -1$, let $x=-2$. $\frac{3(-2)+1}{1+(-2)} = \frac{-5}{-1} = 5 > 0$. The inequality holds.
• For $-1 < x \le -1/3$, let $x=-0.5$. $\frac{3(-0.5)+1}{1+(-0.5)} = \frac{-0.5}{0.5} = -1 \le 0$. The inequality does not hold in the interior, but holds at $x=-1/3$.
• For $x > -1/3$, let $x=0$. $\frac{3(0)+1}{1+0} = \frac{1}{1} = 1 > 0$. The inequality holds.

So, the solution to the first inequality is $x \in (-\infty, -1) \cup [-1/3, \infty)$.

2. $\frac{2x}{1+x} \le 1$

$\frac{2x}{1+x} - 1 \le 0$

$\frac{2x - (1+x)}{1+x} \le 0$

$\frac{x - 1}{1+x} \le 0$

This inequality holds when the numerator and denominator have opposite signs, or when the numerator is zero.

The critical points are where the numerator or denominator is zero: $x-1=0 \implies x = 1$, and $1+x=0 \implies x = -1$.

We analyze the sign of the expression $\frac{x-1}{1+x}$ in the intervals determined by these points: $(-\infty, -1)$, $(-1, 1]$, $[1, \infty)$.

• For $x < -1$, let $x=-2$. $\frac{-2-1}{1+(-2)} = \frac{-3}{-1} = 3 > 0$. The inequality does not hold.
• For $-1 < x \le 1$, let $x=0$. $\frac{0-1}{1+0} = \frac{-1}{1} = -1 \le 0$. The inequality holds.
• For $x > 1$, let $x=2$. $\frac{2-1}{1+2} = \frac{1}{3} > 0$. The inequality does not hold.

So, the solution to the second inequality is $x \in (-1, 1]$.

The domain of $f(x)$ is the intersection of the solutions to both inequalities.

Intersection of $(-\infty, -1) \cup [-1/3, \infty)$ and $(-1, 1]$.

The intersection is $[-1/3, 1]$.

The condition $x \ne -1$ is satisfied by this interval.

Domain of $f(x) = \arccos \frac{2x}{1+x}$ is $[-1/3, 1]$.

(ii) $f(x) = \sqrt{\cos(\sin x)} + \sin^{-1} \frac{1+x^2}{2x}$

For the function to be defined, both terms must be defined.

Term 1: $\sqrt{\cos(\sin x)}$

For the square root to be defined, the expression inside the square root must be non-negative:

$\cos(\sin x) \ge 0$.

The range of $\sin x$ is $[-1, 1]$. Let $y = \sin x$, so $y \in [-1, 1]$.

We need to find the values of $y \in [-1, 1]$ for which $\cos y \ge 0$.

The cosine function is non-negative in the interval $[-\pi/2, \pi/2]$ and its periodic repetitions.

Since $-1 \le y \le 1$ and $-\pi/2 \approx -1.57$ and $\pi/2 \approx 1.57$, the interval $[-1, 1]$ is a subset of $[-\pi/2, \pi/2]$.

In the interval $[-\pi/2, \pi/2]$, $\cos y \ge 0$.

Since $\sin x$ always lies in $[-1, 1]$, which is a subset of $[-\pi/2, \pi/2]$, $\cos(\sin x)$ is always non-negative for any real $x$.

Thus, the domain of $\sqrt{\cos(\sin x)}$ is $\mathbb{R}$.

Term 2: $\sin^{-1} \frac{1+x^2}{2x}$

For the inverse sine function to be defined, the argument must be in the interval $[-1, 1]$:

$-1 \le \frac{1+x^2}{2x} \le 1$

Also, the denominator cannot be zero, so $2x \ne 0$, which means $x \ne 0$.

We split the inequality into two parts:

1. $\frac{1+x^2}{2x} \ge -1$

$\frac{1+x^2}{2x} + 1 \ge 0$

$\frac{1+x^2 + 2x}{2x} \ge 0$

$\frac{(x+1)^2}{2x} \ge 0$

The numerator $(x+1)^2$ is always non-negative for real $x$. For the fraction to be non-negative, the denominator $2x$ must be positive, or the numerator must be zero.

$2x > 0 \implies x > 0$.

$(x+1)^2 = 0 \implies x = -1$.

So, the solution to the first inequality is $x \in (0, \infty) \cup \{-1\}$.

2. $\frac{1+x^2}{2x} \le 1$

$\frac{1+x^2}{2x} - 1 \le 0$

$\frac{1+x^2 - 2x}{2x} \le 0$

$\frac{(x-1)^2}{2x} \le 0$

The numerator $(x-1)^2$ is always non-negative for real $x$. For the fraction to be non-positive, the denominator $2x$ must be negative, or the numerator must be zero.

$2x < 0 \implies x < 0$.

$(x-1)^2 = 0 \implies x = 1$.

So, the solution to the second inequality is $x \in (-\infty, 0) \cup \{1\}$.

The domain of $\sin^{-1} \frac{1+x^2}{2x}$ is the intersection of the solutions to both inequalities, excluding $x=0$.

Intersection of $((0, \infty) \cup \{-1\})$ and $((-\infty, 0) \cup \{1\})$.

Let's check the elements in the intersection:

• The element $-1$ is in $(0, \infty) \cup \{-1\}$ and in $(-\infty, 0) \cup \{1\}$. So $-1$ is in the intersection.
• The element $1$ is in $(0, \infty) \cup \{-1\}$ (since $1 \in (0, \infty)$) and in $(-\infty, 0) \cup \{1\}$. So $1$ is in the intersection.
• The interval $(0, \infty)$ has no intersection with $(-\infty, 0)$.

The intersection is $\{-1, 1\}$.

The condition $x \ne 0$ is satisfied by this set.

Thus, the domain of $\sin^{-1} \frac{1+x^2}{2x}$ is $\{-1, 1\}$.

The domain of the entire function $f(x) = \sqrt{\cos(\sin x)} + \sin^{-1} \frac{1+x^2}{2x}$ is the intersection of the domains of the two terms.

Domain of $\sqrt{\cos(\sin x)}$ is $\mathbb{R}$.

Domain of $\sin^{-1} \frac{1+x^2}{2x}$ is $\{-1, 1\}$.

The intersection of $\mathbb{R}$ and $\{-1, 1\}$ is $\{-1, 1\}$.

Domain of $f(x) = \sqrt{\cos(\sin x)} + \sin^{-1} \frac{1+x^2}{2x}$ is $\{-1, 1\}$.

The final answer is $\boxed{(i) [-1/3, 1], (ii) \{-1, 1\}}$.