Question

Differentiate the following with respect to x:

$(x^2 + 4x + 1)^3 + (x^3 - 5x - 2)^4$

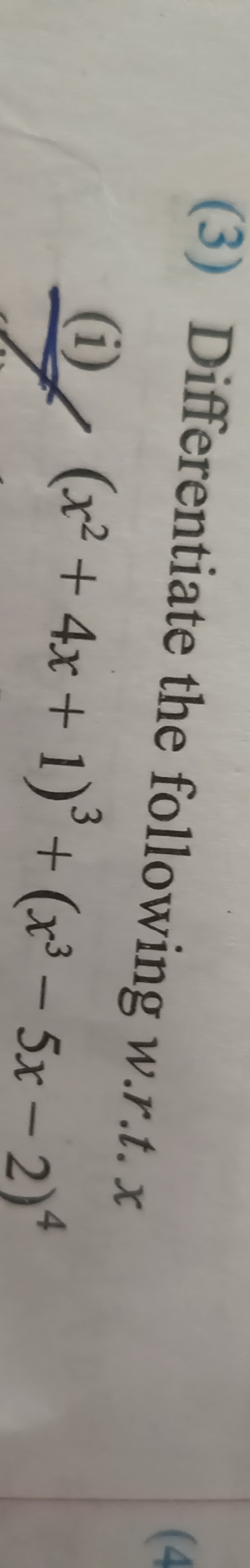
Answer 1

3(2x+4)(x^2+4x+1)^2 + 4(3x^2-5)(x^3-5x-2)^3

Answer 2

Differentiate each term using the Chain Rule.

1. For $(x^2 + 4x + 1)^3$:

$\frac{d}{dx}\left[(x^2 + 4x + 1)^3\right] = 3(x^2+4x+1)^2 \cdot \frac{d}{dx}(x^2+4x+1)$

and

$\frac{d}{dx}(x^2+4x+1)= 2x+4$.

Thus, the derivative is:

$3(2x+4)(x^2+4x+1)^2$.

2. For $(x^3 - 5x - 2)^4$:

$\frac{d}{dx}\left[(x^3-5x-2)^4\right] = 4(x^3-5x-2)^3 \cdot \frac{d}{dx}(x^3-5x-2)$

and

$\frac{d}{dx}(x^3-5x-2)= 3x^2-5$.

Thus, the derivative is:

$4(3x^2-5)(x^3-5x-2)^3$.

Core Explanation

• Apply the Chain Rule to each term.
• Differentiate the outer function and multiply by the derivative of the inner function.