Question

Calculate the amount of He (in gm) present in the 10 litre container at 240 atm and 300K. Given value of "b" for He is 0.08 dm³ mol¯¹. (R = 0.08 atm lit mol' K¯¹)

Answer 1

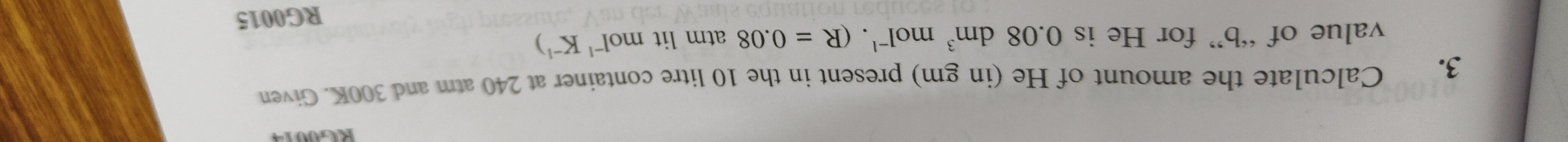
2000/9 gm

Answer 2

The van der Waals equation for a real gas is $(P + \frac{an^2}{V^2})(V - nb) = nRT$. Given that 'a' is not provided and pressure is high, we can approximate the equation to $P(V - nb) = nRT$. We are given: $V = 10$ L $P = 240$ atm $T = 300$ K $b = 0.08$ dm³ mol⁻¹ = $0.08$ L mol⁻¹ $R = 0.08$ atm L mol⁻¹ K⁻¹

Rearranging the simplified equation to solve for $n$: $n = \frac{PV}{RT + Pb}$

Calculate the terms: $RT = (0.08 \text{ atm L mol}^{-1} \text{ K}^{-1}) \times (300 \text{ K}) = 24 \text{ atm L mol}^{-1}$ $Pb = (240 \text{ atm}) \times (0.08 \text{ L mol}^{-1}) = 19.2 \text{ atm L mol}^{-1}$ $PV = (240 \text{ atm}) \times (10 \text{ L}) = 2400 \text{ atm L}$

Substitute these values: $n = \frac{2400 \text{ atm L}}{24 \text{ atm L mol}^{-1} + 19.2 \text{ atm L mol}^{-1}} = \frac{2400}{43.2} \text{ mol} = \frac{500}{9} \text{ mol}$

The molar mass of Helium (He) is approximately 4 g/mol. Mass ($m$) = $n \times M = \frac{500}{9} \text{ mol} \times 4 \text{ g/mol} = \frac{2000}{9} \text{ g}$.