Question
Question: $\begin{vmatrix} a^2 & 2ab & b^2 \\ b^2 & a^2 & 2ab \\ 2ab & b^2 & a^2 \end{vmatrix} = (a^3 + b^3)^2...
a2b22ab2aba2b2b22aba2=(a3+b3)2
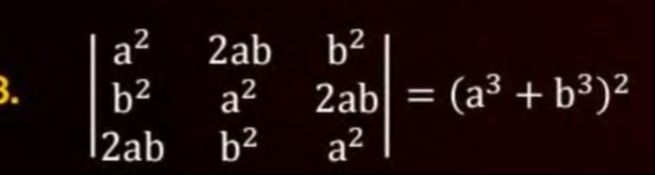
(a3+b3)2
Solution
Let the given determinant be D.
D=a2b22ab2aba2b2b22aba2
This is a cyclic determinant of the form xzyyxzzyx, where x=a2, y=2ab, and z=b2.
The value of a 3×3 cyclic determinant is given by the formula:
xzyyxzzyx=(x+y+z)(x2+y2+z2−xy−yz−zx).
Substitute the values of x,y,z:
x+y+z=a2+2ab+b2=(a+b)2.
x2=(a2)2=a4 y2=(2ab)2=4a2b2 z2=(b2)2=b4 xy=a2(2ab)=2a3b yz=(2ab)(b2)=2ab3 zx=b2(a2)=a2b2
Now calculate x2+y2+z2−xy−yz−zx:
a4+4a2b2+b4−2a3b−2ab3−a2b2
=a4−2a3b+(4a2b2−a2b2)−2ab3+b4
=a4−2a3b+3a2b2−2ab3+b4.
This expression is the expansion of (a2−ab+b2)2:
(a2−ab+b2)2=((a2+b2)−ab)2=(a2+b2)2−2(a2+b2)(ab)+(ab)2
=(a4+2a2b2+b4)−(2a3b+2ab3)+a2b2
=a4+2a2b2+b4−2a3b−2ab3+a2b2
=a4−2a3b+3a2b2−2ab3+b4.
So, x2+y2+z2−xy−yz−zx=(a2−ab+b2)2.
Now, substitute these back into the determinant formula:
D=(x+y+z)(x2+y2+z2−xy−yz−zx)
D=(a+b)2(a2−ab+b2)2
D=[(a+b)(a2−ab+b2)]2
Recall the sum of cubes formula: a3+b3=(a+b)(a2−ab+b2).
So, D=(a3+b3)2.
The given statement is a2b22ab2aba2b2b22aba2=(a3+b3)2.
Our calculation shows that the determinant is indeed equal to (a3+b3)2.
Thus, the statement is true.
