Question

A uniform rod AB of length $l$ can slide between the floor and the wall as shown in the figure. If the end A is moving with uniform velocity $v_A$ away from the wall, find the:

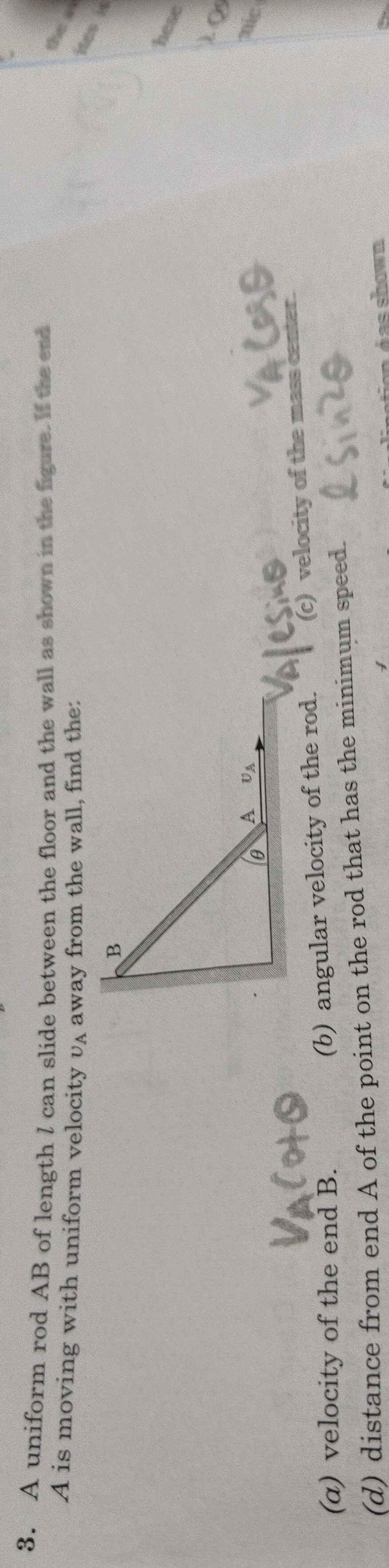
• A. velocity of the end B.
• B. angular velocity of the rod.
• C. velocity of the mass center.
• D. distance from end A of the point on the rod that has the minimum speed.

Answer 1

Answer: (A), (D)

a, d

Answer 2

1. Coordinate System and Kinematic Relations: Set up a coordinate system with the origin at the wall-floor corner. Let end A be at $(x,0)$ and end B at $(0,y)$. The rod length $l$ implies $x^2 + y^2 = l^2$. Also, from trigonometry, $x = l \cos\theta$ and $y = l \sin\theta$. Given $\frac{dx}{dt} = v_A$.

2. Velocity of End B: Differentiate $x^2 + y^2 = l^2$ with respect to time to get $2x\frac{dx}{dt} + 2y\frac{dy}{dt} = 0$. Substitute $\frac{dx}{dt} = v_A$ and $\frac{dy}{dt} = v_B$. Solve for $v_B$ and substitute $x = l \cos\theta$, $y = l \sin\theta$ to get $v_B = -v_A \cot\theta$. Magnitude is $v_A \cot\theta$.

3. Angular Velocity: Differentiate $x = l \cos\theta$ with respect to time to get $\frac{dx}{dt} = -l \sin\theta \frac{d\theta}{dt}$. Substitute $\frac{dx}{dt} = v_A$ and $\frac{d\theta}{dt} = \omega$. Solve for $\omega$ to get $\omega = -\frac{v_A}{l \sin\theta}$. Magnitude is $\frac{v_A}{l \sin\theta}$.

4. Velocity of Mass Center: The mass center is at the midpoint $(x/2, y/2)$. Differentiate these coordinates to find $v_{Gx} = \frac{v_A}{2}$ and $v_{Gy} = \frac{v_B}{2} = -\frac{v_A \cot\theta}{2}$. The magnitude $v_{CM} = \sqrt{v_{Gx}^2 + v_{Gy}^2} = \frac{v_A}{2\sin\theta}$.

5. Point of Minimum Speed: Let P be a point at distance $r$ from A. Use the section formula to find its coordinates: $P_x = \frac{(l-r)x}{l}$ and $P_y = \frac{ry}{l}$. Differentiate these to find $v_{Px}$ and $v_{Py}$. Calculate $v_P^2 = v_{Px}^2 + v_{Py}^2$. Minimize $v_P^2$ by differentiating with respect to $r$ and setting the derivative to zero. This yields $r = l \sin^2\theta$.