Question

A hyperbola passing through origin has 3x-4y-1=0 and 4x-3y-6=0 as its asymptotes. Then equation of its transverse and conjugate axes are

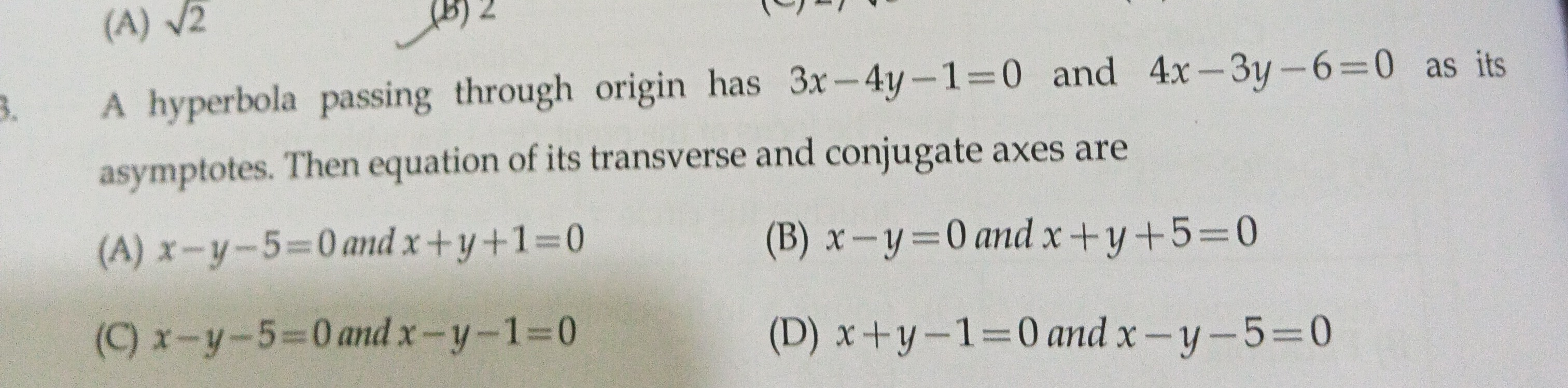
• A. x-y-5=0 and x+y+1=0
• B. x-y=0 and x+y+5=0
• C. x-y-5=0 and x-y-1=0
• D. x+y-5=0 and x-y-1=0

Answer 1

Answer: (D)

(D)

Answer 2

The given asymptotes of the hyperbola are $L_1 = 3x - 4y - 1 = 0$ and $L_2 = 4x - 3y - 6 = 0$.

The equation of a hyperbola with asymptotes $L_1 = 0$ and $L_2 = 0$ is given by $L_1 L_2 = k$, where $k$ is a constant.

So, the equation of the hyperbola is $(3x - 4y - 1)(4x - 3y - 6) = k$.

Since the hyperbola passes through the origin (0, 0), we can substitute $x=0$ and $y=0$ into the equation to find the value of $k$: $(3(0) - 4(0) - 1)(4(0) - 3(0) - 6) = k$ $(-1)(-6) = k$ $k = 6$.

The equation of the hyperbola is $(3x - 4y - 1)(4x - 3y - 6) = 6$.

The center of the hyperbola is the point of intersection of the asymptotes. We solve the system of equations:

1. $3x - 4y = 1$
2. $4x - 3y = 6$ Multiply equation (1) by 3: $9x - 12y = 3$. Multiply equation (2) by 4: $16x - 12y = 24$. Subtract the first modified equation from the second: $(16x - 12y) - (9x - 12y) = 24 - 3 \implies 7x = 21 \implies x = 3$. Substitute $x=3$ into equation (1): $3(3) - 4y = 1 \implies 9 - 4y = 1 \implies 4y = 8 \implies y = 2$. The center of the hyperbola is (3, 2).

The transverse and conjugate axes are the angle bisectors of the asymptotes and pass through the center. The equations of the angle bisectors of $a_1x + b_1y + c_1 = 0$ and $a_2x + b_2y + c_2 = 0$ are given by $\frac{a_1x + b_1y + c_1}{\sqrt{a_1^2 + b_1^2}} = \pm \frac{a_2x + b_2y + c_2}{\sqrt{a_2^2 + b_2^2}}$. For $L_1 = 3x - 4y - 1 = 0$, $\sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5$. For $L_2 = 4x - 3y - 6 = 0$, $\sqrt{4^2 + (-3)^2} = \sqrt{16 + 9} = \sqrt{25} = 5$. The equations of the angle bisectors are: $\frac{3x - 4y - 1}{5} = \pm \frac{4x - 3y - 6}{5}$ $3x - 4y - 1 = \pm (4x - 3y - 6)$.

Case 1: $3x - 4y - 1 = 4x - 3y - 6$ $0 = 4x - 3x - 3y + 4y - 6 + 1$ $0 = x + y - 5$ $x + y - 5 = 0$.

Case 2: $3x - 4y - 1 = -(4x - 3y - 6)$ $3x - 4y - 1 = -4x + 3y + 6$ $3x + 4x - 4y - 3y - 1 - 6 = 0$ $7x - 7y - 7 = 0$ Dividing by 7, we get $x - y - 1 = 0$.

The equations of the axes are $x + y - 5 = 0$ and $x - y - 1 = 0$.

To determine which one is the transverse axis and which one is the conjugate axis, we consider the equation of the hyperbola relative to its center (3, 2). Let $X = x - 3$ and $Y = y - 2$. $3x - 4y - 1 = 3(X+3) - 4(Y+2) - 1 = 3X + 9 - 4Y - 8 - 1 = 3X - 4Y$. $4x - 3y - 6 = 4(X+3) - 3(Y+2) - 6 = 4X + 12 - 3Y - 6 - 6 = 4X - 3Y$. The equation of the hyperbola is $(3X - 4Y)(4X - 3Y) = 6$.

The axes relative to the center are $X + Y = 0$ and $X - Y = 0$. Let $U = X - Y$ and $V = X + Y$. Then $X = (U+V)/2$ and $Y = (V-U)/2$. $3X - 4Y = 3(U+V)/2 - 4(V-U)/2 = (3U + 3V - 4V + 4U)/2 = (7U - V)/2$. $4X - 3Y = 4(U+V)/2 - 3(V-U)/2 = (4U + 4V - 3V + 3U)/2 = (7U + V)/2$. Substituting these into the hyperbola equation: $\left(\frac{7U - V}{2}\right)\left(\frac{7U + V}{2}\right) = 6$ $\frac{(7U)^2 - V^2}{4} = 6$ $49U^2 - V^2 = 24$. Dividing by 24, we get $\frac{49U^2}{24} - \frac{V^2}{24} = 1$, or $\frac{U^2}{24/49} - \frac{V^2}{24} = 1$. This is in the standard form $\frac{u^2}{a^2} - \frac{v^2}{b^2} = 1$, where $u = U = X - Y$ and $v = V = X + Y$. In this form, the transverse axis is the line $v=0$ and the conjugate axis is the line $u=0$. So, the transverse axis is $V = X + Y = 0$, which is $(x - 3) + (y - 2) = 0 \implies x + y - 5 = 0$. The conjugate axis is $U = X - Y = 0$, which is $(x - 3) - (y - 2) = 0 \implies x - y - 1 = 0$.

Thus, the equation of the transverse axis is $x + y - 5 = 0$ and the equation of the conjugate axis is $x - y - 1 = 0$.