Question

A radioactive substance disintegrates to 1/16th of its original mass in 160 days. Then, its half life period is

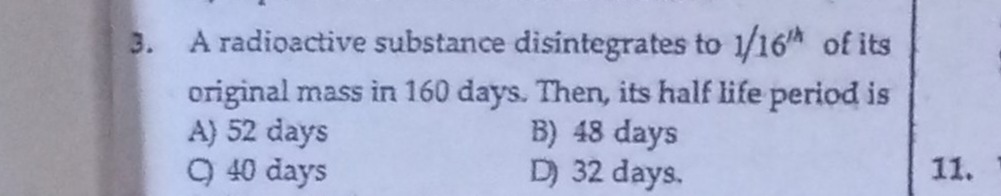
• A. 52 days
• B. 48 days
• C. 40 days
• D. 32 days

Answer 1

Answer: (C)

40 days

Answer 2

The decay law is given by

$$\frac{N}{N_{0}}=\left(\frac{1}{2}\right)^{\frac{t}{T_{1/2}}}.$$

We have $\frac{N}{N_0}=\frac{1}{16}$ when $t=160$ days. Since

$$\frac{1}{16}=\left(\frac{1}{2}\right)^4,$$

we set

$$\frac{160}{T_{1/2}}=4 \quad \Rightarrow \quad T_{1/2}=\frac{160}{4}=40 \text{ days}.$$

Core Explanation:

• Use the decay law $\frac{N}{N_0} = (1/2)^{t/T_{1/2}}$.
• $1/16=(1/2)^4$ so there are 4 half-lives in 160 days.
• Therefore, $T_{1/2} = 160/4 = 40$ days.