Question

A particle of mass m is released from rest a distance b from a fixed origin of force that attracts the particle according to the inverse square law $F(x) = -kx^{-2}$. The time required for the particle to reach the origin is given by $\pi (\frac{mb^3}{\alpha K})^{\frac{1}{2}}$. The value of $\alpha$ is:

Answer 1

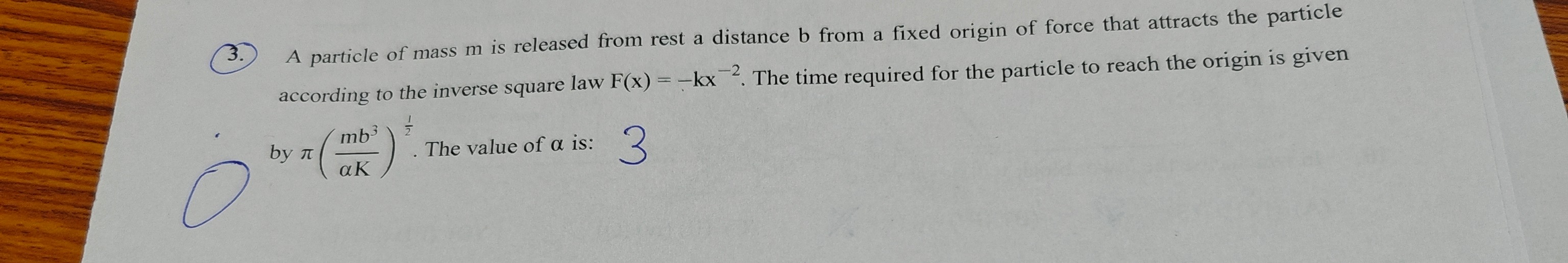
8

Answer 2

The problem asks for the value of $\alpha$ given the time taken for a particle to reach the origin under an inverse square law attractive force.

1. Set up the equation of motion: The force acting on the particle is $F(x) = -kx^{-2}$. According to Newton's second law, $F = ma$, so: $m \frac{d^2x}{dt^2} = -kx^{-2}$

2. Express acceleration in terms of velocity and position: We can write $\frac{d^2x}{dt^2} = \frac{dv}{dt} = \frac{dv}{dx} \frac{dx}{dt} = v \frac{dv}{dx}$. Substituting this into the equation of motion: $mv \frac{dv}{dx} = -kx^{-2}$

3. Integrate to find velocity as a function of position: Separate variables and integrate. The particle is released from rest ($v=0$) at $x=b$. $\int_{0}^{v} mv' dv' = \int_{b}^{x} -k (x')^{-2} dx'$ $\frac{1}{2}mv^2 - 0 = -k \left[ -\frac{1}{x'} \right]_{b}^{x}$ $\frac{1}{2}mv^2 = k \left( \frac{1}{x} - \frac{1}{b} \right)$ $\frac{1}{2}mv^2 = k \frac{b-x}{bx}$ $v^2 = \frac{2k}{m} \frac{b-x}{bx}$

4. Determine the sign of velocity and set up the integral for time: Since the particle is attracted to the origin, its position $x$ decreases with time. Therefore, $\frac{dx}{dt}$ must be negative. $v = \frac{dx}{dt} = -\sqrt{\frac{2k}{m}} \sqrt{\frac{b-x}{bx}}$ Rearrange to find $dt$: $dt = -\sqrt{\frac{m}{2k}} \sqrt{\frac{bx}{b-x}} dx$

5. Integrate to find the total time: The particle starts at $x=b$ at $t=0$ and reaches the origin ($x=0$) at time $T$. $T = \int_{0}^{T} dt = \int_{b}^{0} -\sqrt{\frac{m}{2k}} \sqrt{\frac{bx}{b-x}} dx$ To simplify the integration, swap the limits and change the sign: $T = \sqrt{\frac{m}{2k}} \int_{0}^{b} \sqrt{\frac{bx}{b-x}} dx$

6. Evaluate the definite integral: Let the integral be $I = \int_{0}^{b} \sqrt{\frac{bx}{b-x}} dx$. Use the trigonometric substitution $x = b\sin^2\theta$. Then $dx = 2b\sin\theta\cos\theta d\theta$. When $x=0$, $\theta=0$. When $x=b$, $\theta=\frac{\pi}{2}$. $\sqrt{\frac{bx}{b-x}} = \sqrt{\frac{b(b\sin^2\theta)}{b-b\sin^2\theta}} = \sqrt{\frac{b^2\sin^2\theta}{b\cos^2\theta}} = \sqrt{b} \frac{\sin\theta}{\cos\theta} = \sqrt{b}\tan\theta$. Substitute these into the integral: $I = \int_{0}^{\pi/2} (\sqrt{b}\tan\theta) (2b\sin\theta\cos\theta) d\theta$ $I = \int_{0}^{\pi/2} 2b\sqrt{b} \sin^2\theta d\theta$ Using the identity $\sin^2\theta = \frac{1-\cos(2\theta)}{2}$: $I = 2b\sqrt{b} \int_{0}^{\pi/2} \frac{1-\cos(2\theta)}{2} d\theta$ $I = b\sqrt{b} \left[ \theta - \frac{1}{2}\sin(2\theta) \right]_{0}^{\pi/2}$ $I = b\sqrt{b} \left[ \left(\frac{\pi}{2} - \frac{1}{2}\sin(\pi)\right) - \left(0 - \frac{1}{2}\sin(0)\right) \right]$ $I = b\sqrt{b} \left[ \frac{\pi}{2} - 0 - 0 + 0 \right] = \frac{\pi b^{3/2}}{2}$

7. Substitute the integral result back into the time expression: $T = \sqrt{\frac{m}{2k}} \cdot \frac{\pi b^{3/2}}{2}$ $T = \frac{\pi}{2\sqrt{2}} \sqrt{\frac{m}{k}} b^{3/2}$ To match the given form, group terms under the square root: $T = \pi \sqrt{\frac{m b^3}{8k}}$ $T = \pi \left( \frac{mb^3}{8k} \right)^{\frac{1}{2}}$

8. Compare with the given formula to find $\alpha$: The given formula is $T = \pi \left( \frac{mb^3}{\alpha K} \right)^{\frac{1}{2}}$. Comparing our derived expression with the given formula, assuming $K=k$: $\alpha = 8$