Question

A particle moves along a vertical circle of radius r with a velocity $\sqrt{7gr}$ at its bottom point A. If $T_A, T_B, T_C$ and $T_D$ represent tensions at A, B, C and D respectively, then

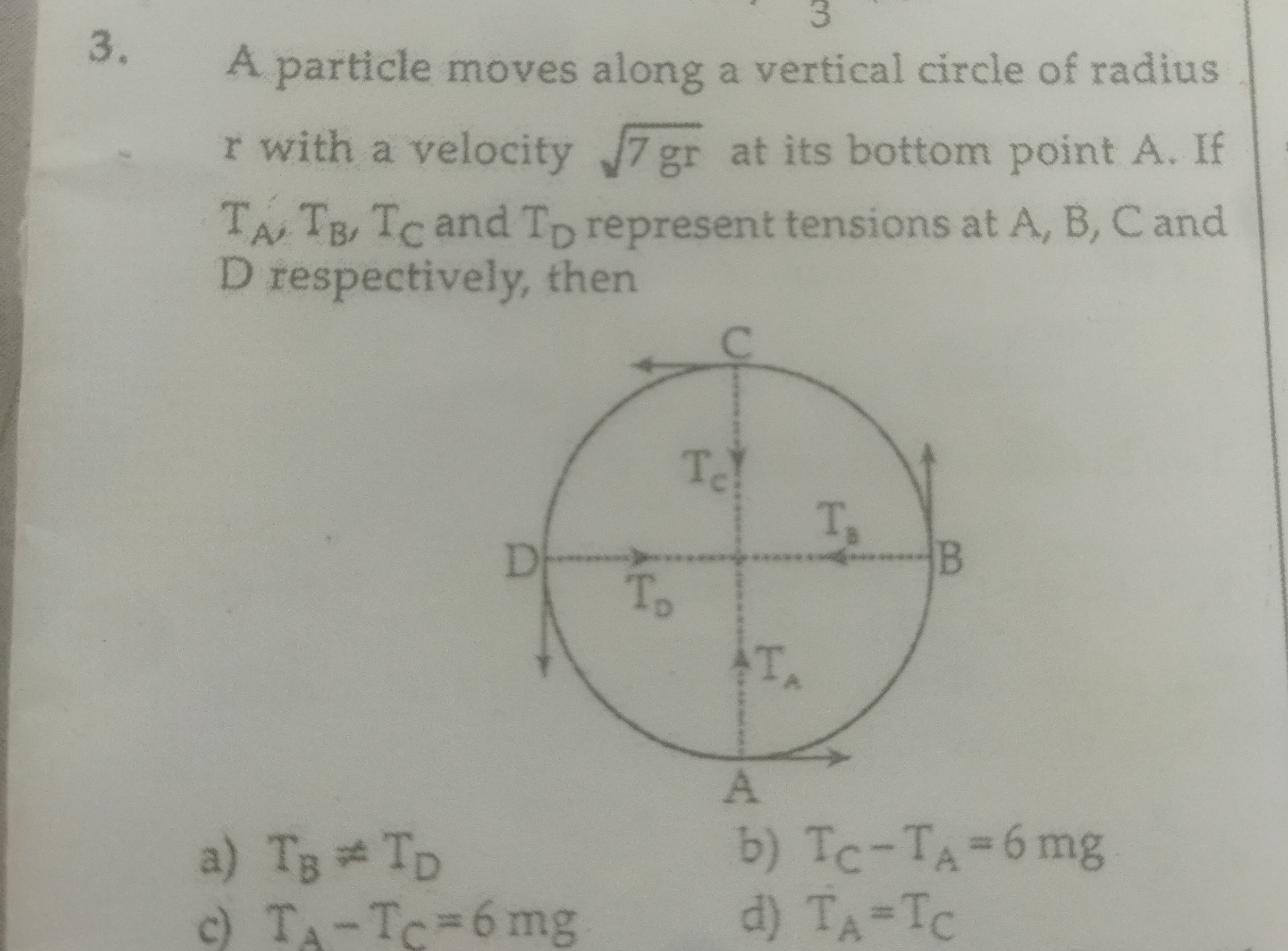
• A. $T_B \neq T_D$
• B. $T_C - T_A = 6mg$
• C. $T_A - T_C = 6mg$
• D. $T_A = T_C$

Answer 1

Answer: (C)

(c) $T_A - T_C = 6mg$

Answer 2

1. Determine speeds using energy conservation:

   • At A (bottom), given:

     $$v_A = \sqrt{7gr}.$$

   • Let A be zero potential energy. Then at:

     • B (rightmost, height = r): $$\frac{1}{2}mv_B^2 = \frac{1}{2}mv_A^2 - mg\,r \quad \Rightarrow \quad v_B^2 = 7gr - 2gr = 5gr.$$
     • C (top, height = 2r): $$v_C^2 = 7gr - 4gr = 3gr.$$
     • D (leftmost, height = r): $$v_D^2 = 5gr \quad (\text{same as B}).$$

2. Apply radial force equations (centripetal force requirement):

   • At A (bottom):
     Here tension $T_A$ acts upward, weight $mg$ acts downward. The net upward force provides centripetal acceleration: $$T_A - mg = \frac{mv_A^2}{r} = \frac{m(7gr)}{r} = 7mg \quad \Rightarrow \quad T_A = 8mg.$$
   • At B (rightmost):
     At B, the radius is horizontal. Tension $T_B$ provides the entire centripetal force since $mg$ (vertical) is perpendicular to the radial direction: $$T_B = \frac{mv_B^2}{r} = 5mg.$$
   • At C (top):
     Both tension $T_C$ and weight $mg$ act downward (towards the center): $$T_C + mg = \frac{mv_C^2}{r} = 3mg \quad \Rightarrow \quad T_C = 2mg.$$
   • At D (leftmost):
     Similar to B (only tension provides centripetal force): $$T_D = \frac{mv_D^2}{r} = 5mg.$$

3. Compare tensions for the options:

   • (a) $T_B \neq T_D$: Actually, $T_B = T_D = 5mg$ — False.
   • (b) $T_C - T_A = 6mg$: $T_C - T_A = 2mg - 8mg = -6mg$ — False.
   • (c) $T_A - T_C = 6mg$: $8mg - 2mg = 6mg$ — True.
   • (d) $T_A = T_C$: $8mg \neq 2mg$ — False.