Question
Question: A parallel plate capacitor has d = 1 mm and C = 1 F with no medium inside will have :...
A parallel plate capacitor has d = 1 mm and C = 1 F with no medium inside will have :
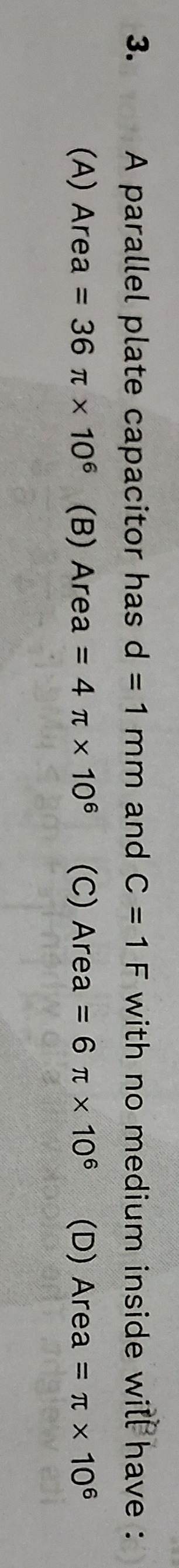
Area = 36 π x 106
Area = 4 π × 106
Area = 6 π× 106
Area = π × 106
Area = 36 π x 106
Solution
The capacitance of a parallel plate capacitor with no medium inside (vacuum or air) is given by the formula:
C=dϵ0A
where C is the capacitance, ϵ0 is the permittivity of free space, A is the area of each plate, and d is the separation between the plates.
We are given:
C=1 F d=1 mm =1×10−3 m
We need to find the area A. Rearranging the formula, we get:
A=ϵ0Cd
The value of ϵ0 is approximately 8.854×10−12 F/m. However, the options are given in terms of π, which suggests using the value of ϵ0 related to the Coulomb constant k=4πϵ01=9×109Nm2/C2.
From this relationship, we can find ϵ0:
ϵ0=4πk1=4π×9×1091=36π×1091=36π10−9 F/m.
Now, substitute the values of C, d, and ϵ0 into the formula for A:
A=36π10−9 F/m(1 F)×(1×10−3 m) A=36π10−91×10−3 m2 A=10−910−3×36π m2 A=36π×10−3−(−9) m2 A=36π×106 m2
